题目内容
14. 如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5.5,CD=3.5,则EF的长是( )
如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5.5,CD=3.5,则EF的长是( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
分析 首先连接CF,并延长交AB于点G,由ASA证得△CDF≌△GBF,即可求得CF=GF,CD=GB=3.5,继而可得EF是△ACG的中位线,则可求得答案.
解答 解:连接CF,并延长交AB于点G,如图所示: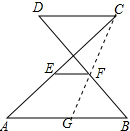
∵AB∥CD,
∴∠CDF=∠GBF,
在△CDF和△GBF中,$\left\{\begin{array}{l}{∠CDF=∠GBF}&{\;}\\{DF=BF}&{\;}\\{∠DFC=∠BFG}&{\;}\end{array}\right.$,
∴△CDF≌△GBF(ASA),
∴CF=GF,CD=GB=3.5,
∴AG=AB-BG=5.5-3.5=2,
又∵E为AC的中点,
∴EF是△ACG的中位线,
∴EF=$\frac{1}{2}$AG=1.
故选:A.
点评 此题考查了全等三角形的判定与性质以及三角形的中位线定理;熟练掌握三角形中位线定理,证明三角形全等是解决问题的关键;注意掌握辅助线的作法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知a,b为正整数,满足ab-2b-a-24=0,则a+b的最大值为( )
| A. | 7 | B. | 18 | C. | 29 | D. | 30 |
5.在△ABC中,∠A:∠B:∠C=1:2:3,最短边BC=4cm,则最长边AB的长是( )
| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
2.若a=240,b=332,c=424,则下列关系正确的是( )
| A. | a>b>c | B. | b>c>a | C. | c>a>b | D. | c>b>a |
9. 如图,△ABC的边BC上的高是( )
如图,△ABC的边BC上的高是( )
 如图,△ABC的边BC上的高是( )
如图,△ABC的边BC上的高是( )| A. | BE | B. | DB | C. | CF | D. | AF |
19.对于某种细菌来说,一个细菌,经过1分钟分裂为2个,再过1分钟,又分别分裂为2个,既总共分裂为4个,…,照这样的分裂速度,若一个细菌分裂成满满一小瓶恰好需要1小时,同样的细菌,同样的分裂速度,同样的小瓶,如果开始时瓶内装有2个细菌,恰好分裂成满满一小瓶需要( )
| A. | 15分钟 | B. | 30分钟 | C. | 58分钟 | D. | 59分钟 |
6.已知Rt△ABC中,∠C=90°,b为∠B的对边,a为∠A的对边,若b与∠A已知,则下列各式正确的是( )
| A. | a=bsin∠A | B. | a=bcos∠A | C. | a=btan∠A | D. | a=b÷tan∠A |
3.如图1是由6个相同的小正方块组成的几何体,移动其中一个小正方块,变成图2所示的几何体,则移动前后( )


| A. | 主视图改变,俯视图改变 | B. | 主视图不变,俯视图改变 | ||
| C. | 主视图不变,俯视图不变 | D. | 主视图改变,俯视图不变 |
4. 如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
 如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )| A. | $\frac{3}{11}$ | B. | $\frac{7}{11}$ | C. | $\frac{11}{3}$ | D. | $\frac{11}{7}$ |