题目内容
19．对于某种细菌来说，一个细菌，经过1分钟分裂为2个，再过1分钟，又分别分裂为2个，既总共分裂为4个，…，照这样的分裂速度，若一个细菌分裂成满满一小瓶恰好需要1小时，同样的细菌，同样的分裂速度，同样的小瓶，如果开始时瓶内装有2个细菌，恰好分裂成满满一小瓶需要（ ）| A． | 15分钟 | B． | 30分钟 | C． | 58分钟 | D． | 59分钟 |
分析 根据题意1分钟分裂成2个，2分钟分裂成4个，n分钟分裂成2n个，一个细菌经过1小时的繁殖充满瓶子，若开始就放2个细菌只须59分钟就能充满瓶子．
解答 解：一个细菌1分钟分裂成2个，2分钟分裂成4个，n分钟分裂成2n个，一个细菌经过1小时的繁殖能使瓶子充满．
如果开始就在瓶子里放入2个细菌，繁殖的速度比原来快一分钟．
故细菌充满瓶子所需要的时间为59分钟．
故选：D．
点评 主要考查了乘方的逆向运用，要根据题意正确地列式．乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．乘方的逆向运用可以倒过来计算．
练习册系列答案
相关题目
9．y=$\frac{\sqrt{3x+1}}{x-1}$的x取值范围是（ ）
| A． | x$≥-\frac{1}{3}$ | B． | x$＞-\frac{1}{3}$且x≠1 | C． | x$≥-\frac{1}{3}$且x≠1 | D． | -$\frac{1}{3}$≤x≤1 |
10．船在静水中的速度为10km/h，水流速度为2km/h，顺流航行s km所需时间为（ ）
| A． | （$\frac{s}{10}$+2）h | B． | （$\frac{s}{10+2}$）h | C． | （$\frac{s}{10}$-2）h | D． | （$\frac{s}{10-2}$）h |
7．
为了加强视力保护意识，小明要在书房里挂一张视力表．由于书房空间狭小，他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表．如图，如果大视力表中“E”的高度是3.5cm，那么小视力表中相应“E”的高度是（ ）
为了加强视力保护意识，小明要在书房里挂一张视力表．由于书房空间狭小，他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表．如图，如果大视力表中“E”的高度是3.5cm，那么小视力表中相应“E”的高度是（ ）| A． | 3cm | B． | 2.5cm | C． | 2.3cm | D． | 2.1cm |
14．
如图，AB∥CD，E，F分别为AC，BD的中点，若AB=5.5，CD=3.5，则EF的长是（ ）
如图，AB∥CD，E，F分别为AC，BD的中点，若AB=5.5，CD=3.5，则EF的长是（ ）| A． | 1 | B． | 1.5 | C． | 2 | D． | 2.5 |
4．
如图，△ABC中，∠C=90°，CD⊥AB于D，图中线段中可以作为△ACD的高的有（ ）
如图，△ABC中，∠C=90°，CD⊥AB于D，图中线段中可以作为△ACD的高的有（ ）| A． | 0条 | B． | 1条 | C． | 2条 | D． | 3条 |
11．
如图，下列关系式错误的是（ ）
如图，下列关系式错误的是（ ）| A． | ∠AOE=2∠AOC | B． | ∠AOC＞∠AOB | C． | ∠COD+∠EOD=∠COE | D． | ∠DOE=∠BOC |
8．
如图，若∠1=∠3，则下列结论一定成立的是（ ）
如图，若∠1=∠3，则下列结论一定成立的是（ ）| A． | ∠1=∠4 | B． | ∠3=∠4 | C． | ∠1+∠2=180° | D． | ∠2+∠4=180° |
9．
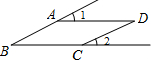如图，∠1=∠B，∠2=25°，则∠D等于（ ）
如图，∠1=∠B，∠2=25°，则∠D等于（ ）| A． | 25° | B． | 30° | C． | 45° | D． | 50° |