题目内容
4. 如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )| A. | $\frac{3}{11}$ | B. | $\frac{7}{11}$ | C. | $\frac{11}{3}$ | D. | $\frac{11}{7}$ |
分析 根据反射的性质,可得β,根据余角的性质,可得∠1与∠2的关系,根据相似三角形的判定与性质,可得CE的长,根据正切函数,可得答案.
解答 解:设CE的长为x,如图, ,
,
由入射角等于反射角,得
∠β=∠α,
由余角的性质,得
∠1=∠2.
由AC⊥CD,BD⊥CD,得
∠ACE=∠BDE,
△ACE∽△BDE,
$\frac{AC}{BD}$=$\frac{CE}{DE}$,即$\frac{3}{x}$=$\frac{4}{11-x}$,
解得x=$\frac{33}{7}$
由题意,得
∠A=∠α.
tanα=tan∠A=$\frac{CE}{AC}$=$\frac{\frac{33}{7}}{3}$=$\frac{11}{7}$,
故选:D.
点评 本题考查了相似三角形的判定与性质,利用相似三角形的判定与性质得出CE的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5.5,CD=3.5,则EF的长是( )
如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5.5,CD=3.5,则EF的长是( )
 如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5.5,CD=3.5,则EF的长是( )
如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5.5,CD=3.5,则EF的长是( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
15.在△ABC中,∠C=90°,若AC=2,BC=4,则AB的长度等于( )
| A. | 3 | B. | $2\sqrt{3}$ | C. | $2\sqrt{5}$ | D. | 以上都不对 |
12.下列四个选项是我省四个城市某天的平均气温,其中平均气温最低的是( )
| A. | -5℃ | B. | -10℃ | C. | -2℃ | D. | 3℃ |
19.在早餐店里,王伯伯花2元买了2个馒头和1个包子,李阿姨花7元买了4个馒头,5个包子.则买1个馒头和1个包子要花( )
| A. | 3元 | B. | 2元 | C. | 1.5元 | D. | 1元 |
9.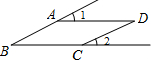 如图,∠1=∠B,∠2=25°,则∠D等于( )
如图,∠1=∠B,∠2=25°,则∠D等于( )
 如图,∠1=∠B,∠2=25°,则∠D等于( )
如图,∠1=∠B,∠2=25°,则∠D等于( )| A. | 25° | B. | 30° | C. | 45° | D. | 50° |
16.若a2-3b=5,则6b-2a2+2016的值是( )
| A. | 2026 | B. | 2016 | C. | 2006 | D. | 2015 |
 小明同学在社团活动中给发明的机器人设置程序:(a,n),机器人执行步骤是:向 正前方走a米后向左转n°,再依次执行相同程序,直至回到原点.现输入a=3,n=60°,那么机器人回到原出发点共走了18米.
小明同学在社团活动中给发明的机器人设置程序:(a,n),机器人执行步骤是:向 正前方走a米后向左转n°,再依次执行相同程序,直至回到原点.现输入a=3,n=60°,那么机器人回到原出发点共走了18米. 如图所示,韩梅家的左右两侧各摆了3盆花,韩梅每次按照以下规则往家中搬一盆花,先选择左侧还是右侧,然后搬该侧离家最近的,要把所有的花搬到家里,共有( )种不同的搬花顺序.
如图所示,韩梅家的左右两侧各摆了3盆花,韩梅每次按照以下规则往家中搬一盆花,先选择左侧还是右侧,然后搬该侧离家最近的,要把所有的花搬到家里,共有( )种不同的搬花顺序.