题目内容
9.已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB、CD之间的距离为7或17cm.分析 分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可,小心别漏解.
解答 解:①当弦AB和CD在圆心同侧时,如图1,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12-5=7cm;
②当弦AB和CD在圆心异侧时,如图2,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴AB与CD之间的距离为7cm或17cm.
故答案为7或17.
点评 本题考查了勾股定理和垂径定理的应用.此题难度适中,解题的关键是注意掌握数形结合思想与分类讨论思想的应用,小心别漏解.

练习册系列答案
相关题目
4.已知圆外一点和圆周的最短距离为2,最长距离为8,则该圆的半径是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
14.下列分式的运算中,正确的是( )
| A. | $\frac{a+x}{a+y}$=$\frac{x}{y}$ | B. | $\frac{{x}^{3}}{{x}^{6}}$=$\frac{1}{{x}^{2}}$ | C. | $\frac{a+b}{a+b}$=0 | D. | $\frac{a}{ab+a}$=$\frac{1}{b+1}$ |
17.下列计算中,正确的是( )
| A. | x3•x3=x6 | B. | x3+x3=x6 | C. | (x3)2=x9 | D. | x6÷x2=x3 |
17.下列各点中,在反比例函数y=$\frac{3}{x}$图象上的点是( )
| A. | ($\frac{1}{3}$,-9) | B. | (3,1) | C. | (-1,3) | D. | (6,-$\frac{1}{2}$) |
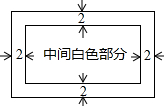 如图,小红用一张周长为88cm的长方形白纸做一张贺卡,长方形白纸内部的四周涂上宽为2cm的彩色花边.
如图,小红用一张周长为88cm的长方形白纸做一张贺卡,长方形白纸内部的四周涂上宽为2cm的彩色花边.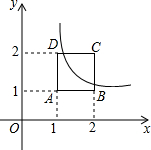 如图,反比例函数y=$\frac{k}{x}$的图象与正方形ABCD在BC和CD边上相交.已知A(1,1),C(2,2),则k的值可能是( )
如图,反比例函数y=$\frac{k}{x}$的图象与正方形ABCD在BC和CD边上相交.已知A(1,1),C(2,2),则k的值可能是( )