题目内容
14.已知平面直角坐标系xOy,反比例函数$y=\frac{60}{x}$的图象上有一点B,其横坐标为15,点C在y轴上,若BC=17,则点C的坐标为(0,12)或(0,-4).分析 首先根据题意画出图形,然后过点B作BE⊥y轴于点E,作BD⊥x轴于点D,由反比例函数y=$\frac{60}{x}$的图象上有一点B,其横坐标为15,可求得BD,BE的长,利用勾股定理,可求得CE的长,继而求得答案.
解答 解:如图,过点B作BE⊥y轴于点E,作BD⊥x轴于点D,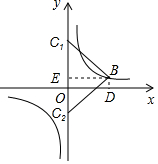
∵反比例函数y=$\frac{60}{x}$的图象上有一点B,其横坐标为15,
∴点B的坐标为:(15,4),
∴BE=15,BD=4,
∵BC=17,
∴EC=$\sqrt{B{C}^{2}-B{E}^{2}}$=8,
∴OC1=4+8=12,OC2=8-4=4,
∴点C的坐标为:(0,12)或(0,-4).
故答案为:(0,12)或(0,-4).
点评 此题考查了反比例函数图象上点的坐标特征以及勾股定理.注意根据题意画出图形,结合图形求解是关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
10.如果在△ABC中,∠A=70°-∠B,则∠C等于( )
| A. | 140° | B. | 110° | C. | 70° | D. | 35° |
6.把△ABC三边的长度都扩大为原来的2倍,则锐角A的正切函数值( )
| A. | 缩小为原来的$\frac{1}{2}$ | B. | 不变 | C. | 扩大为原来的2倍 | D. | 扩大为原来的4倍 |
 如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为70cm2.
如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为70cm2. 如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是121.75米.
如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是121.75米.