题目内容
5.$\sqrt{\frac{81}{16}}$的平方根是$±\frac{3}{2}$;$\sqrt{{{({\sqrt{3}-2})}^2}}$=2-$\sqrt{3}$.
分析 先求出$\sqrt{\frac{81}{16}}$的值,再根据平方根的定义即可得出答案;
先判断出$\sqrt{3}$-2<0,再根据$\sqrt{{a}^{2}}$(a≤0)=-a,即可得出答案.
解答 解:∵$\sqrt{\frac{81}{16}}$=$\frac{9}{4}$
∴$\sqrt{\frac{81}{16}}$的平方根是±$\frac{3}{2}$;
∵$\sqrt{3}$-2<0,
∴$\sqrt{(\sqrt{3}-2)^{2}}$=2-$\sqrt{3}$;
故答案为:±$\frac{3}{2}$,2-$\sqrt{3}$.
点评 此题考查了平方根和算术平方根,熟练掌握平方根和算术平方根的定义是解题的关键,是一道基础题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
4.下列说法不正确的是( )
| A. | 0既不是正数也不是负数 | |
| B. | 有理数可以分为正有理数,负有理数和零 | |
| C. | 0的绝对值等于它的相反数 | |
| D. | 任意一个有理数的绝对值都是正数 |
2.如果3x2myn+1与-$\frac{1}{2}$x2ym+3是同类项,则m,n的值为( )
| A. | m=-1,n=3 | B. | m=1,n=3 | C. | m=-1,n=-3 | D. | m=1,n=-3 |
10.下列分式中,属于最简分式的是( )
| A. | $\frac{4}{2x}$ | B. | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | C. | $\frac{{x}^{2}-36}{2x+12}$ | D. | $\frac{1-x}{x-1}$ |
17. 如图,四边形ABCD是边长为4的正方形,点E为边BC上的点,以DE为边向外作矩形DEFG,使FG过点A,若DG=$\frac{16}{5}$,那么DE=( )
如图,四边形ABCD是边长为4的正方形,点E为边BC上的点,以DE为边向外作矩形DEFG,使FG过点A,若DG=$\frac{16}{5}$,那么DE=( )
 如图,四边形ABCD是边长为4的正方形,点E为边BC上的点,以DE为边向外作矩形DEFG,使FG过点A,若DG=$\frac{16}{5}$,那么DE=( )
如图,四边形ABCD是边长为4的正方形,点E为边BC上的点,以DE为边向外作矩形DEFG,使FG过点A,若DG=$\frac{16}{5}$,那么DE=( )| A. | 5 | B. | 3$\sqrt{2}$ | C. | $\frac{32}{5}$ | D. | $\frac{28}{5}$ |
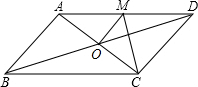 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是10cm,则?ABCD的周长为20cm.
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是10cm,则?ABCD的周长为20cm.