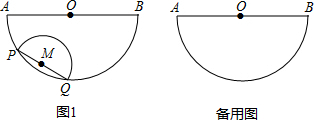
题目内容
2．
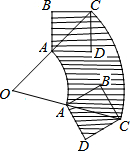如图所示，正方形ABCD对角线AC所在直线上有一点O，OA=AC=2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是2π+2．
分析 如图，用大扇形的面积减去小扇形的面积再加上正方形ABCD的面积．
解答 解：∵OA=AC=2，
∴AB=BC=CD=AD=$\sqrt{2}$，OC=4，
S阴影=$\frac{60°}{360°}π{（4}^{2}{-2}^{2}）$+${（\sqrt{2}）}^{2}$=2π+2，
故答案为：2π+2．
点评 此题考查了扇形的面积公式和旋转的性质以及勾股定理，能够把不规则图形的面积转换为规则图形的面积是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12．在一个凸n边形的纸板上切下一个三角形后，剩下的一个内角和为1080°的多边形，则n的值为（ ）
| A． | 7 | B． | 8 | C． | 9 | D． | 以上都有可能 |
7．已知△ABC顶点坐标分别是A（0，6），B（-3，-3），C（1，0），将△ABC平移后顶点A的对应点A1的坐标是（4，10），则点B的对应点B1的坐标为（ ）
| A． | （7，1） | B． | B（1，7） | C． | （1，1） | D． | （2，1） |
14．
如图，直线a，b被直线c所截，若a∥b，∠1=110°，则∠2等于（ ）
如图，直线a，b被直线c所截，若a∥b，∠1=110°，则∠2等于（ ）| A． | 70° | B． | 75° | C． | 80° | D． | 85° |