题目内容
19.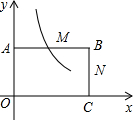 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(4,2),M、N分别是AB、BC的中点.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(4,2),M、N分别是AB、BC的中点.(1)若反比例函数y=$\frac{m}{x}$(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(2)若反比例函数y=$\frac{m}{x}$(x>0)的图象与△MNB(包括边界)有公共点,请直接写出m的取值范围.
分析 (1)根据顶点B的坐标为(4,2),M、N分别是AB、BC的中点.得到M点的坐标为(2,2),把M(2,2)代入反比例函数y=$\frac{m}{x}$(m≠0)可求出m,确定反比例函数的解析式;再根据B点坐标为(4,2),N点坐标为(4,1),易得N(4,1)满足反比例函数解析式,即可判断点N在该函数的图象上;
(2)由反比例函数y=$\frac{m}{x}$(m≠0)的图象与△BMN的边始终有公共点,而M、N都在y=$\frac{4}{x}$上,则此时m最小,反比例函数过B点时,m最大,此时m=4×2=8,由此得到m的取值范围.
解答 解:(1)∵顶点B的坐标为(4,2),M、N分别是AB、BC的中点,
∴M点的坐标为(2,2),
把M(2,2)代入反比例函数y=$\frac{m}{x}$(m≠0)得,m=2×2=4,
∴反比例函数的解析式为y=$\frac{4}{x}$;
∵M、N分别为矩形OABC的边AB、BC的中点,且M(2,2),B点坐标为(4,2),
∴N点坐标为(4,1),
∵4×1=4,
∴点N在函数y=$\frac{4}{x}$的图象上;
(2)4≤m≤8.
点评 本题考查了反比例函数综合题:点在反比例函数图象上,点的横纵坐标满足其解析式;运用矩形的性质和中点的定义求点的坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列多项式的计算中,可以用平方差公式的是( )
| A. | (x+1)•(2+x) | B. | ($\frac{1}{2}$a+b)•(b-$\frac{1}{2}$a) | C. | (-a+b)•(a-2b) | D. | (-x-$\frac{1}{2}$y)•($\frac{1}{2}$x+y) |
14.某公司近经过市场调研,决定下月对甲、乙两种产品进行“限产压库”,公司决定这两种产品下月共生产20件,这20件产品的产值y不少于1140万元,不多于1200万元.已知有关数据如表:
(1)若生产甲产品x(x为正整数)件,写出x满足的不等式组;
(2)请你帮助公司设计出所有符合题意的生产方案;
(3)若从节省工时数考虑,通过计算,你认为哪种方案最好?
| 产品 | 每件产品的产量 | 每件产品用工时数 |
| 甲 | 45万元 | 150 |
| 乙 | 75万元 | 190 |
(2)请你帮助公司设计出所有符合题意的生产方案;
(3)若从节省工时数考虑,通过计算,你认为哪种方案最好?
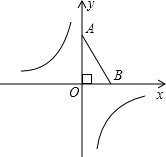 如图,平面直角坐标系中,已知点O(0,0),A(0,2),B(1,0),双曲线y=-$\frac{1}{x}$,动点P在双曲线上,PQ⊥x轴于Q,若△OPQ与△OAB相似,则满足题意的点P一共有($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).
如图,平面直角坐标系中,已知点O(0,0),A(0,2),B(1,0),双曲线y=-$\frac{1}{x}$,动点P在双曲线上,PQ⊥x轴于Q,若△OPQ与△OAB相似,则满足题意的点P一共有($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).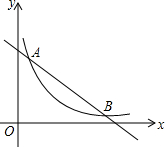 如图,在平面直角坐标系中,A,B两点的纵坐标分别为7和1,直线AB与y轴所夹锐角为60°.
如图,在平面直角坐标系中,A,B两点的纵坐标分别为7和1,直线AB与y轴所夹锐角为60°. 如图,AO=CO,DO=BO,∠COA=∠DOB,求证:△AOB≌△COD.
如图,AO=CO,DO=BO,∠COA=∠DOB,求证:△AOB≌△COD.