题目内容
8. 如图,⊙O与△ABC各边分别切于点D,E,F,
如图,⊙O与△ABC各边分别切于点D,E,F,(1)若∠C=60°,∠EOF=100°,求∠B的度数.
(2)若AB=10cm,AC=8cm,BC=7cm,△ABC的面积是50cm2,求⊙O的半径.
分析 (1)利用切线的性质得OF⊥AB,OE⊥AC,则利用四边形内角和得∠A+∠EOF=180°,所以∠A=80°,然后根据三角形内角和求∠B的度数;
(2)连接OD,OA、OB、OC,如图,设⊙O的半径为r,则OD=OE=OF=r,利用切线的性质得OD⊥BC,然后根据三角形面积公式,利用S△ABC=S△OAB+S△OBC+S△OAC得到$\frac{1}{2}$•10•r+$\frac{1}{2}$•7•r+$\frac{1}{2}$•8•r=50,然后解关于r的方程即可.
解答 解:(1)∵AB、AC与⊙O相切于点F、E,
∴OF⊥AB,OE⊥AC,
∴∠A+∠EOF=180°,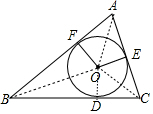
∴∠A=180°-100°=80°,
∵∠A+∠B+∠C=180°,
∴∠B=180°-60°-80°=40°;
(2)连接OD,OA、OB、OC,如图,设⊙O的半径为r,则OD=OE=OF=r,
∵BC与⊙O相切于D,
∴OD⊥BC,
∵S△ABC=S△OAB+S△OBC+S△OAC,
∴$\frac{1}{2}$•10•r+$\frac{1}{2}$•7•r+$\frac{1}{2}$•8•r=50,解得r=4,
即⊙O的半径为4cm.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了三角形面积公式.

练习册系列答案
相关题目
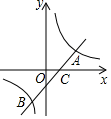 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1). 已知:如图,在梯形ABCD中,∠C=∠D=90°,AD=m,BC=n,点E在CD上,且∠AEB=90°,AE=BE.
已知:如图,在梯形ABCD中,∠C=∠D=90°,AD=m,BC=n,点E在CD上,且∠AEB=90°,AE=BE. 如图所示的相似四边形中,求未知边x的长度和角度α的大小及这两个图形的相似比k.
如图所示的相似四边形中,求未知边x的长度和角度α的大小及这两个图形的相似比k.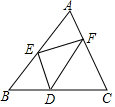 如图,已知D为△ABC的BC边上的一点,DE∥AC交AB于E,DF∥AB交AC于F,求证:△AEF面积为△BDE面积和△CDF面积的比例中项.
如图,已知D为△ABC的BC边上的一点,DE∥AC交AB于E,DF∥AB交AC于F,求证:△AEF面积为△BDE面积和△CDF面积的比例中项. 你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm 2)的反比例函数,其图象如图所示.
你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm 2)的反比例函数,其图象如图所示.