题目内容
嘉淇同学用配方法推导一元二次方程ax2+bx+c=0（a≠0）的求根公式时，对于b2-4ac＞0的情况，她是这样做的：
由于a≠0，方程ax2+bx+c=0变形为：
x2+
x=-
，…第一步
x2+
x+（
）2=-
+（
）2，…第二步
（x+
）2=
，…第三步
x+
=
（b2-4ac＞0），…第四步
x=
，…第五步
嘉淇的解法从第 步开始出现错误；事实上，当b2-4ac＞0时，方程ax2+bx+c=0（a≠O）的求根公式是 ．
用配方法解方程：x2-2x-24=0．
由于a≠0，方程ax2+bx+c=0变形为：
x2+
| b |
| a |
| c |
| a |
x2+
| b |
| a |
| b |
| 2a |
| c |
| a |
| b |
| 2a |
（x+
| b |
| 2a |
| b2-4ac |
| 4a2 |
x+
| b |
| 2a |
| ||
| 4a |
x=
-b+
| ||
| 2a |
嘉淇的解法从第
用配方法解方程：x2-2x-24=0．
考点：解一元二次方程-配方法
专题：阅读型
分析：第四步，开方时出错；把常数项24移项后，应该在左右两边同时加上一次项系数-2的一半的平方．
解答：解：在第四步中，开方应该是x+
=±
．所以求根公式为：x=
．
故答案是：四；x=
；
用配方法解方程：x2-2x-24=0
解：移项，得
x2-2x=24，
配方，得
x2-2x+1=24+1，
即（x-1）2=25，
开方得x-1=±5，
∴x1=6，x2=-4．
| b |
| 2a |
| ||
| 2a |
-b±
| ||
| 2a |
故答案是：四；x=
-b±
| ||
| 2a |
用配方法解方程：x2-2x-24=0
解：移项，得
x2-2x=24，
配方，得
x2-2x+1=24+1，
即（x-1）2=25，
开方得x-1=±5，
∴x1=6，x2=-4．
点评：本题考查了解一元二次方程--配方法．
用配方法解一元二次方程的步骤：
（1）形如x2+px+q=0型：第一步移项，把常数项移到右边；第二步配方，左右两边加上一次项系数一半的平方；第三步左边写成完全平方式；第四步，直接开方即可．
（2）形如ax2+bx+c=0型，方程两边同时除以二次项系数，即化成x2+px+q=0，然后配方．
用配方法解一元二次方程的步骤：
（1）形如x2+px+q=0型：第一步移项，把常数项移到右边；第二步配方，左右两边加上一次项系数一半的平方；第三步左边写成完全平方式；第四步，直接开方即可．
（2）形如ax2+bx+c=0型，方程两边同时除以二次项系数，即化成x2+px+q=0，然后配方．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
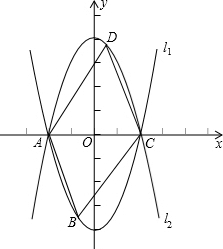如图，已知抛物线l1：y=x2-4与x轴相交于A，C两点．