题目内容
已知两个实数,其中一个比另一个大2,设其中较小的数为x,这两个实数的乘积为y,
(Ⅰ)用含有x的代数式表示较大的数为 (直接填在横线上);
(Ⅱ)y与x的函数关系式为y= (直接填在横线上);
(Ⅲ)这两个数各为多少时它们的乘积最小?
(Ⅰ)用含有x的代数式表示较大的数为
(Ⅱ)y与x的函数关系式为y=
(Ⅲ)这两个数各为多少时它们的乘积最小?
考点:二次函数的最值,列代数式
专题:
分析:(Ⅰ)用较小的数加上2即可;
(Ⅱ)根据y等于这两个数的积整理即可;
(Ⅲ)把函数关系式整理成顶点式形式,然后根据二次函数的最值问题解答.
(Ⅱ)根据y等于这两个数的积整理即可;
(Ⅲ)把函数关系式整理成顶点式形式,然后根据二次函数的最值问题解答.
解答:解:(Ⅰ)较大的数为x+2;
(Ⅱ)y与x的函数关系式为y=x(x+2),
即y=x2+2x;
(Ⅲ)∵y=x2+2x=(x+1)2-1,
∴当x=-1时,y有最小值,
此时,x=-1,x+2=-1+2=1,
所以,这两个数为-1和1时,它们的乘积最小.
故答案为:x+2;x2+2x.
(Ⅱ)y与x的函数关系式为y=x(x+2),
即y=x2+2x;
(Ⅲ)∵y=x2+2x=(x+1)2-1,
∴当x=-1时,y有最小值,
此时,x=-1,x+2=-1+2=1,
所以,这两个数为-1和1时,它们的乘积最小.
故答案为:x+2;x2+2x.
点评:本题考查了二次函数的最值问题,列代数式,整理成顶点式形式求最值更简便.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
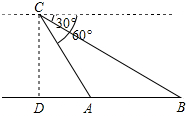 某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
 在△ABC和△A′B′C′中,CD、C′D′平分∠ACB、∠A′C′B′,且CD=C′D′,AB=A′B′,∠ADC=∠A′D′C′,你能判断△ABC≌△A′B′C′吗?
在△ABC和△A′B′C′中,CD、C′D′平分∠ACB、∠A′C′B′,且CD=C′D′,AB=A′B′,∠ADC=∠A′D′C′,你能判断△ABC≌△A′B′C′吗? 如图,抛物线y=-
如图,抛物线y=-