题目内容
12. 如图,矩形OABC在平面直角坐标系中,点B的坐标为(4,3),直线l:y=-2x+b经过点A交x轴于点G.
如图,矩形OABC在平面直角坐标系中,点B的坐标为(4,3),直线l:y=-2x+b经过点A交x轴于点G.(1)直接填空:b=3;
(2)直线l上有一个动点P.
①试探究|PB-PC|的最大值,并说明理由;
②若点P的横坐标为a(0<a≤4),且△ACP的面积为S,试求S与a的函数关系式.
分析 (1)由矩形OABC在平面直角坐标系中,点B的坐标为(4,3),得出A点坐标,再把A点坐标代入y=-2x+b求解即可,
(2)①利用三角形三边关系可得|PB-PC|<BC,只有当点B、C、P在同一直线上时|PB-PC|的最大值,
②先利用勾股定理求出AP的长,过点C作CD⊥AG于点D,再求出OG,CG利用三角函数值得出CD的值,再运用三角形的面积公式求解即可.
解答 解:(1)∵矩形OABC在平面直角坐标系中,点B的坐标为(4,3),
∴A(0,3),
∵y=-2x+b经过点A,
∴把A(0,3)代入y=-2x+b得b=3,
故答案为:3.
(2)①如图1,连接BP,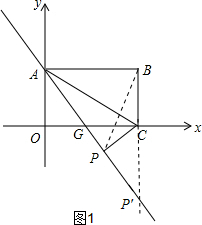
由三角形三边关系可得|PB-PC|<BC,
延长BC交AG于点P′,只有当P运动到点P′时,|PB-PC|=BC=3,
所以|PB-PC|的最大值为4.
②∵点P的横坐标为a,l的解析式为y=-2x+3,
∴P(a,-2a+3).
∴AP=$\sqrt{{a}^{2}+[3-(-2a+3)]^{2}}$=$\sqrt{5}$a,
如图2,过点C作CD⊥AG于点D,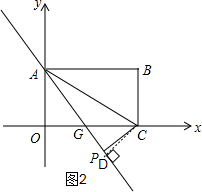
∵y=-2x+3交x轴于点G.
∴G($\frac{3}{2}$,0),
∴OG=$\frac{3}{2}$,CG=4-$\frac{3}{2}$=$\frac{5}{2}$,AG=$\sqrt{A{O}^{2}+O{G}^{2}}$=$\frac{3\sqrt{5}}{2}$,
∴sin∠AGO=$\frac{AO}{AG}$=$\frac{3}{\frac{3\sqrt{5}}{2}}$=$\frac{2\sqrt{5}}{5}$,
∵sin∠CGD=$\frac{CD}{CG}$=$\frac{CD}{\frac{5}{2}}$=$\frac{2\sqrt{5}}{5}$,
∴CD=$\sqrt{5}$,
∴S=$\frac{1}{2}$AP•CD=$\frac{1}{2}$×$\sqrt{5}$a×$\sqrt{5}$=$\frac{5}{2}$a.
点评 本题主要考查了一次函数的综合题,涉及一次函数的解析式,最值及三角函数问题上,解题的关键是灵活作出辅助线,正确的求出三角形的高与底.

 如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为2$\sqrt{3}$.
如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为2$\sqrt{3}$.
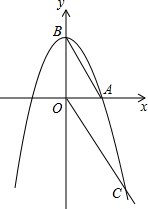 如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.
如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.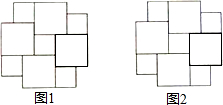 如图是以两个大小不同的正方形为基本图案镶嵌而成的图形,请仅用无刻度的直尺按不同的方法分别在图1、图2中画一个正方形,使它的面积等于这两个大小不同的正方形的面积之和.要求:(1)用虚线连线;(2)要标注你所画正方形的顶点字母.
如图是以两个大小不同的正方形为基本图案镶嵌而成的图形,请仅用无刻度的直尺按不同的方法分别在图1、图2中画一个正方形,使它的面积等于这两个大小不同的正方形的面积之和.要求:(1)用虚线连线;(2)要标注你所画正方形的顶点字母.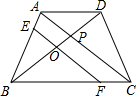 如图,在梯形ABCD中,AD∥BC,BC=2AD,O是BD的中点,过点O作EF∥AC交AB于E,交BC于F,若AC=16cm,求EF的长度.
如图,在梯形ABCD中,AD∥BC,BC=2AD,O是BD的中点,过点O作EF∥AC交AB于E,交BC于F,若AC=16cm,求EF的长度.