题目内容
 如图,∠AOB=90°,OB是∠COD的平分线,OE为CO的延长线.
如图,∠AOB=90°,OB是∠COD的平分线,OE为CO的延长线.(1)当∠AOC=50°时,求∠DOE的度数;
(2)当∠AOC=80°时,求∠DOE的度数;
(3)通过(1)、(2)的计算,请你猜想∠AOC和∠DOE的数量关系,并说明理由.
考点:角平分线的定义
专题:
分析:(1)先由∠AOB=90°,∠AOC=50°,可得∠BOC=∠AOB-∠AOC=40°,由OB是∠COD的平分线,得出∠COD=2∠BOC=80°,再根据邻补角定义即可求出∠DOE=180°-∠COD=100°;
(2)先由∠AOB=90°,∠AOC=80°,可得∠BOC=∠AOB-∠AOC=10°,由OB是∠COD的平分线,得出∠COD=2∠BOC=20°,再根据邻补角定义即可求出∠DOE=180°-∠COD=160°;
(3)通过(1)、(2)的计算,可以猜想∠AOC和∠DOE的数量关系是∠DOE=2∠AOC.先由∠AOB=90°,可得∠BOC=∠AOB-∠AOC=90°-∠AOC,由OB是∠COD的平分线,得出∠COD=2∠BOC=2(90°-∠AOC)=180°-2∠AOC,再根据邻补角定义即可求出∠DOE=180°-∠COD=180°-(180°-2∠AOC)=2∠AOC.
(2)先由∠AOB=90°,∠AOC=80°,可得∠BOC=∠AOB-∠AOC=10°,由OB是∠COD的平分线,得出∠COD=2∠BOC=20°,再根据邻补角定义即可求出∠DOE=180°-∠COD=160°;
(3)通过(1)、(2)的计算,可以猜想∠AOC和∠DOE的数量关系是∠DOE=2∠AOC.先由∠AOB=90°,可得∠BOC=∠AOB-∠AOC=90°-∠AOC,由OB是∠COD的平分线,得出∠COD=2∠BOC=2(90°-∠AOC)=180°-2∠AOC,再根据邻补角定义即可求出∠DOE=180°-∠COD=180°-(180°-2∠AOC)=2∠AOC.
解答:解:(1)∵∠AOB=90°,∠AOC=50°,
∴∠BOC=∠AOB-∠AOC=40°,
∵OB是∠COD的平分线,
∴∠COD=2∠BOC=80°,
∴∠DOE=180°-∠COD=100°;
(2)∵∠AOB=90°,∠AOC=80°,
∴∠BOC=∠AOB-∠AOC=10°,
∵OB是∠COD的平分线,
∴∠COD=2∠BOC=20°,
∴∠DOE=180°-∠COD=160°;
(3)猜想∠DOE=2∠AOC.
∵∠AOB=90°,
∴∠BOC=∠AOB-∠AOC=90°-∠AOC,
∵OB是∠COD的平分线,
∴∠COD=2∠BOC=2(90°-∠AOC)=180°-2∠AOC,
∴∠DOE=180°-∠COD=180°-(180°-2∠AOC)=2∠AOC.
∴∠BOC=∠AOB-∠AOC=40°,
∵OB是∠COD的平分线,
∴∠COD=2∠BOC=80°,
∴∠DOE=180°-∠COD=100°;
(2)∵∠AOB=90°,∠AOC=80°,
∴∠BOC=∠AOB-∠AOC=10°,
∵OB是∠COD的平分线,
∴∠COD=2∠BOC=20°,
∴∠DOE=180°-∠COD=160°;
(3)猜想∠DOE=2∠AOC.
∵∠AOB=90°,
∴∠BOC=∠AOB-∠AOC=90°-∠AOC,
∵OB是∠COD的平分线,
∴∠COD=2∠BOC=2(90°-∠AOC)=180°-2∠AOC,
∴∠DOE=180°-∠COD=180°-(180°-2∠AOC)=2∠AOC.
点评:本题考查了角的平分线定义和角的有关计算的应用,主要考查学生计算能力和推理能力,求解过程类似.

练习册系列答案
相关题目
 从正面观察如图的两个物体,看到的是( )
从正面观察如图的两个物体,看到的是( )A、 |
B、 |
C、 |
D、 |
 二次函数y=ax2+bx+c的图象如图所示,下列结论:①c<0;②b>0;③4a+2b+c>0;④b2-4ac>0.其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①c<0;②b>0;③4a+2b+c>0;④b2-4ac>0.其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
已知命题“关于x的方程bx+1=0必有解”,能说明这个命题是假命题的一个反例是( )
| A、b=-1 | B、b=2 |
| C、b=-2 | D、b=0 |
 如图,AD平分∠BAC,BD⊥AD,DE∥AC,求证:△BDE是等腰三角形.
如图,AD平分∠BAC,BD⊥AD,DE∥AC,求证:△BDE是等腰三角形.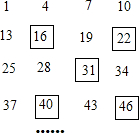 将一定规律的一组数1,4,7,10,13…排成如下表,并象如图一样对称框住其中五个数(阴影部分),请你仔细观察框住的五个数字规律,并回答下列问题:
将一定规律的一组数1,4,7,10,13…排成如下表,并象如图一样对称框住其中五个数(阴影部分),请你仔细观察框住的五个数字规律,并回答下列问题: 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).请按要求分别完成下列各小题:
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).请按要求分别完成下列各小题: