题目内容
18．
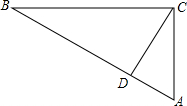已知：如图，在△ABC中，∠A=60°，CD⊥AB，BC=2CD，AD=$\sqrt{3}$，求AB的长．
分析 利用锐角三角三角函数关系进而得出∠B的度数，进而得出∠BCA=90°，分别得出DC，BD的长即可得出答案．
解答 解：∵CD⊥AB，BC=2CD，
∴sinB=$\frac{1}{2}$，
∴∠B=30°，
∴∠BCA=90°，
设DC=x，则tan60°=$\frac{DC}{AD}$=$\frac{x}{\sqrt{3}}$，
解得：x=3，
故tan30°=$\frac{DC}{BD}$=$\frac{3}{BD}$，
解得：BD=3$\sqrt{3}$，
则AB的长为：BD+AD=4$\sqrt{3}$．
点评 此题主要考查了勾股定理以及锐角三角三角函数关系，得出∠B=30°进而求出DC的长是解题关键．
练习册系列答案
相关题目
如图，Rt△ABC中，直角边是AC、BC，斜边是AB．
13．三角形的三边情况是①a=5，b=12，c=9，②a=15，b=17，c=8，③a=1，b=$2\sqrt{2}$，c=3，④a：b：c=5：12：13，其中直角三角形有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |