题目内容
如图,△ABC内部有若干个点,用这些点以及△ABC的顶点A,B,C把原三角形分割成一些三角形(互相不重叠).

(1)填写下表:
(2)如果用y表示内部有n个点时,△ABC被分割成的三角形的个数,试写出y与n的关系式;
(3)原△ABC能否被分割成2006个三角形?若能,求此时△ABC内部有多少个点?若不能,请说明理由.

(1)填写下表:
| △ABC内点的个数 | 1 | 2 | 3 | 4 |
| 分割成的三角形的个数 | 3 | 5 |
(3)原△ABC能否被分割成2006个三角形?若能,求此时△ABC内部有多少个点?若不能,请说明理由.
考点:规律型:图形的变化类
专题:
分析:(1)观察图形,不难发现:内部每多一个点,则多2个三角形;
(2)根据(1)的发现,则易写出y=3+2(n-1);
(3)根据(2)的结论,列方程求解.
(2)根据(1)的发现,则易写出y=3+2(n-1);
(3)根据(2)的结论,列方程求解.
解答:解:(1)填表:
(2)y=3+2(n-1)=2n+1;
(3)若△ABC能被分割成2006个三角形,则2n+1=2006.
n=
,不是整数.
所以,原三角形不能被分割成2006个三角形.
| △ABC内点的个数 | 1 | 2 | 3 | 4 |
| 分割成的三角形的个数 | 3 | 5 | 7 | 9 |
(3)若△ABC能被分割成2006个三角形,则2n+1=2006.
n=
| 2005 |
| 2 |
所以,原三角形不能被分割成2006个三角形.
点评:此题考查了图形的变化类问题,解题的关键是要结合图形,能够从特殊推广到一般,建立函数关系式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若一个数m用四舍五入法取近似值为2.8,则( )
| A、m=2.80 |
| B、2.75≤m≤2.84 |
| C、2.75<m≤2.84 |
| D、2.75≤m<2.85 |
 已知:如图,点A、E、F、C在同一直线上,AD∥BC,AD=CB,AE=CF.求证:∠B=∠D.
已知:如图,点A、E、F、C在同一直线上,AD∥BC,AD=CB,AE=CF.求证:∠B=∠D. 实数a,b,c在数轴上的位置如图,请化简:|c|-
实数a,b,c在数轴上的位置如图,请化简:|c|-
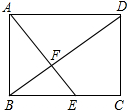 如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.
如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.