题目内容
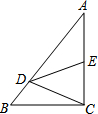如图，在Rt△ABC中，∠C=90°，点D在边AB上，线段DC绕点D逆时针旋转，端点C恰巧落在边AC上的点E处．如果| AD |
| DB |
| AE |
| EC |
考点：平行线分线段成比例,旋转的性质
专题：计算题
分析：作DH⊥AC于H，如图，根据旋转的性质得DE=DC，则利用等腰三角形的性质得EH=CH，由
=n可得AE=2nEH=2nCH，再根据平行线分线段成比例，由DH∥BC得到
=
，所以m=
，然后用等线段代换后约分即可．
| AE |
| EC |
| AD |
| DB |
| AH |
| HC |
| AE+EH |
| HC |
解答：解：作DH⊥AC于H，如图，
∵线段DC绕点D逆时针旋转，端点C恰巧落在边AC上的点E处，
∴DE=DC，
∴EH=CH，
∵
=n，即AE=nEC，
∴AE=2nEH=2nCH，
∵∠C=90°，
∴DH∥BC，
∴
=
，即m=
=
=2n+1．
故答案为：2n+1．
∵线段DC绕点D逆时针旋转，端点C恰巧落在边AC上的点E处，
∴DE=DC，
∴EH=CH，
∵
| AE |
| EC |
∴AE=2nEH=2nCH，
∵∠C=90°，
∴DH∥BC，
∴
| AD |
| DB |
| AH |
| HC |
| AE+EH |
| HC |
| 2nCH+CH |
| CH |
故答案为：2n+1．
点评：本题考查了平行线分线段成比例定理的应用，解此题的关键是能根据定理得出比例式，注意：一组平行线截两条直线，所截得的线段对应成比例．也考查了旋转的性质和等腰三角形的性质．
练习册系列答案
相关题目
相反数是3的数是（ ）
A、-
| ||
B、
| ||
| C、3 | ||
| D、-3 |
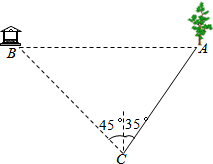如图7，某人在C处看到远处有一凉亭B，在凉亭B正东方向有一棵大树A，这时此人在C处测得B在北偏西45°方向上，测得A在北偏东35°方向上．又测得A、C之间的距离为100米，求A、B之间的距离．（精确到1米）．（参考数据：sin35°≈0.574，cos35°≈0.819，tan35°≈0.700）若四边形的两条对角线相等且互相垂直平分，则这个四边形是（ ）
| A、正方形 | B、菱形 |
| C、矩形 | D、不能确定 |