题目内容
如果关于x的函数y=ax2+(a+2)x+a+1的图象与x轴只有一个公共点,求实数a的值.
考点:抛物线与x轴的交点
专题:计算题
分析:分类讨论:当a=0时,原函数化为一次函数,而已次函数与x轴只有一个公共点;当a≠0时,函数y=ax2+(a+2)x+a+1为二次函数,根据抛物线与x轴的交点问题,当△=(a+2)2-4a(a+1)=0时,它的图象与x轴只有一个公共点,然后解关于a的一元二次方程得到a的值,最后综合两种情况即可得到实数a的值.
解答:解:当a=0时,函数解析式化为y=2x+1,此一次函数与x轴只有一个公共点;
当a≠0时,函数y=ax2+(a+2)x+a+1为二次函数,当△=(a+2)2-4a(a+1)=0时,它的图象与x轴只有一个公共点,
整理得3a2-4=0,解得a=±
,
综上所述,实数a的值为0或±
.
当a≠0时,函数y=ax2+(a+2)x+a+1为二次函数,当△=(a+2)2-4a(a+1)=0时,它的图象与x轴只有一个公共点,
整理得3a2-4=0,解得a=±
2
| ||
| 3 |
综上所述,实数a的值为0或±
2
| ||
| 3 |
点评:本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:当△=b2-4ac>0时,抛物线与x轴有2个交点;当△=b2-4ac=0时,抛物线与x轴有1个交点;当△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
不等式组
的解集是( )
|
| A、x≤3 | B、x≥3 |
| C、1<x≤3 | D、x>1 |
 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
 如图,反比例函数y1=
如图,反比例函数y1=| k1 |
| x |
| A、-1<x<0 |
| B、-1<x<1 |
| C、x<-1或0<x<1 |
| D、-1<x<0或x>1 |
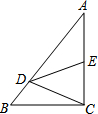 如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果
如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果