题目内容
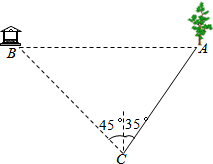 如图7,某人在C处看到远处有一凉亭B,在凉亭B正东方向有一棵大树A,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)
如图7,某人在C处看到远处有一凉亭B,在凉亭B正东方向有一棵大树A,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过点C⊥AB于点D,在Rt△ACD中,求出AD、CD的值,然后在Rt△BCD中求出BD的长度,继而可求得AB的长度.
解答:解:过点C⊥AB于点D,
在Rt△ACD中,
∵∠ACD=35°,AC=100m,
∴AD=100•sin∠ACD=100×0.574=57.4(m),
CD=100•cos∠ACD=100×0.819=81.9(m),
在Rt△BCD中,
∵∠BCD=45°,
∴BD=CD=81.9m,
则AB=AD+BD=57.4+81.9≈139(m).
答:A、B之间的距离约为139米.

在Rt△ACD中,
∵∠ACD=35°,AC=100m,
∴AD=100•sin∠ACD=100×0.574=57.4(m),
CD=100•cos∠ACD=100×0.819=81.9(m),
在Rt△BCD中,
∵∠BCD=45°,
∴BD=CD=81.9m,
则AB=AD+BD=57.4+81.9≈139(m).
答:A、B之间的距离约为139米.
点评:本题考查了直角三角形的应用,解答本题的关键是根据方向角构造直角三角形,利用三角函数解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知Rt△ABC中,∠C=90°,∠CAB=α,AC=7,那么BC为( )
| A、7sinα |
| B、7cosα |
| C、7tanα |
| D、7cotα |
|-
|的相反数是( )
| 1 |
| 3 |
A、
| ||
B、-
| ||
| C、-3 | ||
| D、3 |
如果□+2=0,那么“□”内应填的实数是( )
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
若关于x的二次函数y=kx2+2x-1的图象与x轴仅有一个公共点,则k的取值范围是( )
| A、k=0 | B、k=-1 |
| C、k>-1 | D、k≠0且k=-1 |
将抛物线y=-2x2向右平移一个单位,再向上平移2个单位后,抛物线的表达式为( )
| A、y=-2(x-1)2+2 |
| B、y=-2(x-1)2-2 |
| C、y=-2(x+1)2+2 |
| D、y=-2(x+1)2-2 |
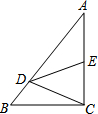 如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果
如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果