题目内容
16.解方程组:(1)$\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=7}\\{\frac{2x}{3}-\frac{y}{4}=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{2}{3}x+\frac{1}{2}y=-\frac{5}{24}}\\{\frac{1}{4}x-\frac{1}{6}y=-\frac{1}{6}}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{\frac{3x-2}{4}+\frac{2y-1}{5}=2}\\{\frac{3x+2}{4}-\frac{3y+1}{5}=0}\end{array}\right.$.
分析 (1)方程组整理后,利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{3x+2y=42①}\\{8x-3y=12②}\end{array}\right.$,
①×3+②×2得:25x=150,即x=6,
把x=6代入①得:y=12,
则方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=12}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{16x+12y=-5①}\\{3x-2y=-2②}\end{array}\right.$,
①+②×6得:34x=-17,即x=-$\frac{1}{2}$,
把x=-$\frac{1}{2}$代入①得:y=$\frac{1}{4}$,
则方程组的解为$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{1}{4}}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{15x+8y=16①}\\{5x-4y=-2②}\end{array}\right.$,
①+②×2得:25x=12,即x=$\frac{12}{25}$,
把x=$\frac{12}{25}$代入②得:$\frac{12}{5}$-4y=-2,即y=$\frac{11}{10}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{12}{25}}\\{y=\frac{11}{10}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案| A. | 5 | B. | 9 | C. | $\sqrt{18}$ | D. | 10$\sqrt{2}$ |
 直线a∥b,点A是直线a上的一个动点,若该点从如图所示的A点出发向右运动,那么△ABC的面积( )
直线a∥b,点A是直线a上的一个动点,若该点从如图所示的A点出发向右运动,那么△ABC的面积( )| A. | 变大 | B. | 变小 | C. | 不变 | D. | 不确定 |

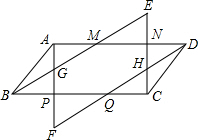 如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF分别交BE、BC、DF于G、P、F点;CE分别交DF、AD、BE于H、N、E点;BE交AD于点M;DF交BC于点K.求证:AF=CE.
如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF分别交BE、BC、DF于G、P、F点;CE分别交DF、AD、BE于H、N、E点;BE交AD于点M;DF交BC于点K.求证:AF=CE. 如图,已知线段a,b和∠α,求作一个三角形,使其有一个内角等于α,且∠α的对边等于a,另一边等于b,要保留作图痕迹,写出作法.
如图,已知线段a,b和∠α,求作一个三角形,使其有一个内角等于α,且∠α的对边等于a,另一边等于b,要保留作图痕迹,写出作法.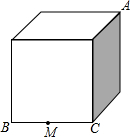 如图正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从A点爬行到M点的最短距离为$\sqrt{13}$.
如图正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从A点爬行到M点的最短距离为$\sqrt{13}$.