题目内容
4.若关于x的方程$\frac{a}{x-1}$=$\frac{1}{2x}$的解为正数,求a的取值范围.分析 分式方程去分母转化为整式方程,表示出x,根据分式方程的解为正数,且最简公分母为0,求出a的范围即可.
解答 解:去分母得:2ax=x-1,即(2a-1)x=-1,
∵分式方程的解为正数,
∴当2a-1≠0,即a≠$\frac{1}{2}$时,解得:x=-$\frac{1}{2a-1}$>0,且-$\frac{1}{2a-1}$≠1,-$\frac{1}{2a-1}$≠0,
则a的范围为a<$\frac{1}{2}$且a≠0.
点评 此题考查了分式方程的解,表示出分式方程的解是解本题的突破点.

练习册系列答案
相关题目
13.已知a>b,则下列结论中错误的是( )
| A. | a-5>b-5 | B. | 2a>2b | C. | a-b>0 | D. | ac>bc |
14.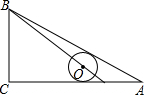 在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
 在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )| A. | 2-$\sqrt{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
 在△ABC中,∠A=$\frac{1}{2}$∠B=∠ACB+20°,CD为∠ACB的平分线,求∠A及∠BDC的度数.
在△ABC中,∠A=$\frac{1}{2}$∠B=∠ACB+20°,CD为∠ACB的平分线,求∠A及∠BDC的度数.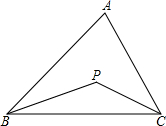 如图所示,BP、CP分别为∠ABC,∠ACB的角平分线,两线交于点P.
如图所示,BP、CP分别为∠ABC,∠ACB的角平分线,两线交于点P.