题目内容
5．
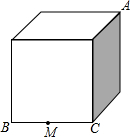如图正方体盒子的棱长为2，BC的中点为M，一只蚂蚁从A点爬行到M点的最短距离为$\sqrt{13}$．
分析 把此正方体的点M所在的面展开，然后在平面内，利用勾股定理求点A和点M间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于2，另一条直角边长等于3，利用勾股定理可求得．
解答 
解：将正方体展开，连接A、M，
根据两点之间线段最短，AM=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$．
答：蚂蚁从A点爬行到M点的最短距离为$\sqrt{13}$．
故答案为：$\sqrt{13}$．
点评 本题考查了勾股定理的拓展应用．“化曲面为平面”是解决“怎样爬行最近”这类问题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
13．已知a＞b，则下列结论中错误的是（ ）
| A． | a-5＞b-5 | B． | 2a＞2b | C． | a-b＞0 | D． | ac＞bc |
20．在实数：-0.3，$\sqrt{1}$，2.010010001…（0的个数依次递增），4.$\stackrel{••}{21}$，2π，$\frac{22}{7}$中，无理数有（ ）
| A． | 1 | B． | 2个 | C． | 3个 | D． | 4个 |
17．把分式$\frac{2a}{a+b}$中的a、b都扩大4倍，则分式的值（ ）
| A． | 扩大8倍 | B． | 不变 | C． | 缩小4倍 | D． | 扩大4倍 |
14．
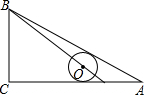在△ABC中，∠C=90°，∠A=30°，BC=1，点P在AC上，∠PBC=45°，⊙O的圆心在线段BP上，且⊙O与AB，AC都相切，则⊙O的半径是（ ）
在△ABC中，∠C=90°，∠A=30°，BC=1，点P在AC上，∠PBC=45°，⊙O的圆心在线段BP上，且⊙O与AB，AC都相切，则⊙O的半径是（ ）| A． | 2-$\sqrt{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | $\frac{\sqrt{3}}{6}$ |
如图，在△ABC中，AG=BG，BD=DE=EC，AC=4AF，若四边形DEFG的面积为11，则△ABC的面积为24．