题目内容
下列说法正确的是( )
A. 掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件
B. 某品牌电插座抽样检查的合格率为99%,说明即使购买1个该品牌的电插座,也可能不合格
C. “明天降雨的概率为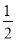
”,表示明天有半天都在降雨
D. 了解一批电视机的使用寿命,适合用普查的方式
B
【解析】解：A．是随机事件，故A错误；
B．正确；
C．错误；
D．了解一批电视机的使用寿命，适合用抽样调查的方式，故D错误．
故选B．
某移动通信公司开设了两种通信业务，“全球通”：使用时首先缴50元月租费，然后每通话1分钟，付话费0.4元；“动感地带”：不缴月租费，每通话1分钟，付话费0.6元(本题的通话均指市内通话)．若一个月通话x分钟，两种方式的费用分别为y1元和y2元．
(1)写出y1，y2与x之间的关系式；
(2)一个月内通话多少分钟，两种方式费用相同？
(3)某人估计一个月内通话300分钟，应选择哪种方式更合算些？
【解析】
(1)y1＝50＋0.4x，y2＝0.6x (2)当每个月通话250分钟时，两种方式费用相同 (3)使用“全球通”合算
【解析】试题分析：（1）理解每种通信业务的付费方式，依据每分钟通话费用×通话时长便可确定每种方式的费用，进而写出y1、y2的关系式；
对于（2），令y1=y2，解方程即可；
对于（3），令x=300，分别求出y1、y2的值，再做比较即可.
【解... 在△ABC中，AB＝AC，且BC＝8cm，BD是腰AC的中线，△ABC的周长分为两部分，已知它们的差为2cm，则等腰三角形的腰长为__________.
10cm或6cm
【解析】如图∵BD是腰AC的中线，
∴AD=CD，
①当△ABD的周长与△BCD的周长差为2时，即AB+AD+BD-(BD+BC+CD)=2,
∴AB-BC=2,
∵BC=8cm，
∴AB=10cm.
②当△BCD的周长与△ABD的周长差为2时，即BD+BC+CD -(AB+AD+BD)=2,
∴BC - AB =2,
∵BC... 在等腰△ABC中，∠A=30°，AB=8，则AB边上的高CD的长是 ．
4或或。
【解析】根据题意画出AB=AC，AB=BC和AC=BC时的图象，然后根据等腰三角形的性质和解直角三角形，分别进行计算即可：
(1)如图，
当AB=AC时，
∵∠A=30°，
∴CD=AC=×8=4。
（2）如图，当AB=BC时，
则∠A=∠ACB=30°。
∴∠ACD=60°。∴∠BCD=30°
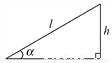
∴CD=cos∠BCD•BC=cos3... 如图，某游乐场一山顶滑梯的高为h，滑梯的坡角为α，那么滑梯长l为( )
A.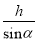 
B. 
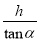C.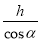 
D. h·sinα
A
【解析】根据锐角三角函数的定义可得，sinα= ，即可得l=，故选A. 下列事件发生的概率为0的是( )
A. 射击运动员只射击1次,就命中靶心
B. 任取一个有理数x,都有|x|≥0
C. 画一个三角形,使其三边的长分别为8 cm,6 cm,2 cm
D. 拋掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
C
【解析】【解析】
A．是随机事件，概率在0-1之间；
B．是必然事件，概率=1；
C．是不可能事件，概率=0；
D．是随机事件，概率在0-1之间．
故选C． 小明家里的阳台地面,水平铺设着仅黑白颜色不同的18块方砖(如图),他从房间里向阳台抛小皮球,小皮球最终随机停留在某块方砖上.
(1)求小皮球分别停留在黑色方砖与白色方砖上的概率.
(2)(1)中哪个概率较大?要使这两个概率相等,应改变哪块方砖的颜色?
（1）， (2)小皮球停留在黑色方砖上的概率大.
【解析】试题分析：（1）根据小球停在黑色方砖上的概率就是黑色方砖面积与总面积的比值，小球停在白色方砖上的概率就是白色方砖面积与总面积的比值，再根据黑色方砖、白色方砖的个数与总个数之间的关系，即可求出答案；
（2）要想这两个概率相等，只要使黑色方砖的个数与白色方砖的个数相等即可．
试题解析：【解析】
（1）∵白色方砖8块，黑色方砖... 一个箱子中放有红、黑、黄三种小球,每个球除颜色外都相同,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢.这个游戏是( )
A. 公平的 B. 先摸者赢的可能性大 C. 不公平的 D. 后摸者赢的可能性大
A
【解析】【解析】
∵一个箱子中放有红、黄、黑三种小球，三个人先后去摸球，一人摸一次，一次摸出一个小球，摸出后放回，∴三个人摸到每种球的概率均相等，故这个游戏是公平的．故选A． 不等式x+3≤6的正整数解为___________________．
x＝1，2，3
【解析】x+3≤6，解得x≤3,故原不等式的正整数解为x＝1，2，3.故答案为x＝1，2，3.