题目内容
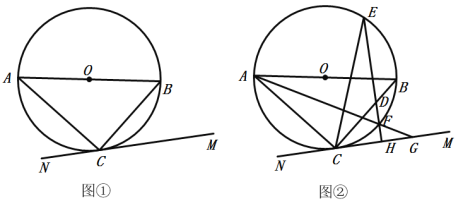
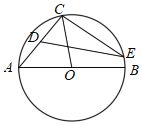
【题目】如图，在
中，
为直径，
，点D为弦
的中点，点E为
上任意一点，则
的大小可能是（ ）
A.
B.
C.
D.
【答案】C
【解析】
连接OD、OE，先求出∠COD=40°，∠BOC=100°，设∠BOE=x，则∠COE=100°-x，∠DOE=100°-x+40°；然后运用等腰三角形的性质分别求得∠OED和∠COE，最后根据线段的和差即可解答．
解：连接OD、OE
∵OC=OA
∴△OAC是等腰三角形
∵
，点D为弦
的中点
∴∠DOC=40°，∠BOC=100°
设∠BOE=x，则∠COE=100°-x，∠DOE=100°-x+40°
∵OC=OE，∠COE=100°-x
∴∠OEC=
∵OD＜OE，∠DOE=100°-x+40°=140°-x
∴∠OED＜
∴∠CED＞∠OEC-∠OED=
=20°．
又∵∠CED＜∠ABC=40°，
故答案为C．
练习册系列答案
相关题目
