题目内容
6.若抛物线y=x2+mx-4的对称轴为直线x=-5,则m的值为10.分析 根据对称轴方程得到-$\frac{m}{2×1}$=-5,然后解关于m的方程即可.
解答 解:根据题意得-$\frac{m}{2×1}$=-5,
解得m=10.
故答案为10.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-b2a时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.

练习册系列答案
相关题目
1.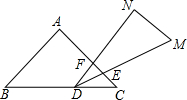 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )| A. | 105° | B. | 115° | C. | 120° | D. | 135° |
16.$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |