题目内容
16.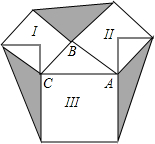 如图,若Rt△ABC的两直边AB=3,BC=2,Ⅰ,Ⅱ,Ⅲ分别表示以AB,BC,AC为边的正方形,则图中三个阴影部分面积之和为9.
如图,若Rt△ABC的两直边AB=3,BC=2,Ⅰ,Ⅱ,Ⅲ分别表示以AB,BC,AC为边的正方形,则图中三个阴影部分面积之和为9.
分析 把△CFH绕点C顺时针旋转90°,使CF与BC重合,H旋转到H'的位置,根据旋转的性质和正方形的性质有A、C、H'在一直线上,且BC为△ABH'的中线,得到S△CHF=S△BCH′=S△ABC,同理:S△BGI=S△ADE=S△ABC,根据三角形的面积公式,可得答案.
解答 解:把△CFH绕点C顺时针旋转90°,使CF与BC重合,H旋转到H'的位置,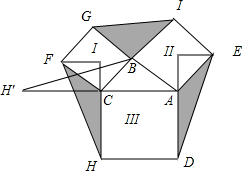 ,
,
∵四边形ACHD为正方形,∠ACH=90°,CA=CH=CH′,
∴A、C、H'在一直线上,且BC为△ABH'的中线,
∴S△CHF=S△BCH′=S△ABC,
同理:S△ADE=S△BGI=S△ABC,
所以阴影部分面积之和为S△ABC的3倍,
又∵AB=3,AC=2,
∴S阴影部分面积=3S△ABC=3×$\frac{1}{2}$AB×AC=3×$\frac{1}{2}$×3×2=9,
故答案为:9.
点评 本题考查了勾股定理,利用了旋转的性质:旋转前后图形全等得出S△CHF=S△BCH′,再利用三角形中线分三角形的面积相等得出S△BCH′=S△ABC是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 如图,该组合体的俯视图是( )
如图,该组合体的俯视图是( )
 如图,该组合体的俯视图是( )
如图,该组合体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5.下列各组二次根式化成最简二次根式后的被开方数完全相同的是( )
| A. | $\sqrt{ab}$与$\sqrt{a{b}^{2}}$ | B. | $\sqrt{mn}$与$\sqrt{\frac{1}{m}+\frac{1}{n}}$ | ||
| C. | $\sqrt{{m}^{2}+{n}^{2}}$与$\sqrt{{m}^{2}-{n}^{2}}$ | D. | $\sqrt{\frac{8}{9}{a}^{3}{b}^{2}}$与$\sqrt{\frac{9}{2}{a}^{3}{b}^{4}}$ |
6.方程$\frac{2x}{{x}^{2}-4}$-$\frac{2}{x-2}$=$\frac{1}{x+2}$的解是( )
| A. | -2 | B. | 2或-2 | C. | 2 | D. | 无解 |
 已知,如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x$+\frac{1}{2}$与x轴交与点A,在第一象限内与反比例函数图象交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求:
已知,如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x$+\frac{1}{2}$与x轴交与点A,在第一象限内与反比例函数图象交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求: