题目内容
7.某学校组织为贫困地区儿童捐资助学的活动,其中七年级捐款总数为1000元,八年级捐款总数比七年级多了20%.已知八年级学生人数比七年级学生人数少25名,而八年级的人均捐款数比七年级的人均捐款数多4元.求七年级学生人均捐款数.分析 设七年级人均捐款数为x元,则八年级人均捐款数为(x+4)元,由八年级学生人数比七年级学生人数少25名建立方程求出其解即可.
解答 解:设七年级人均捐款数为x元,则八年级人均捐款数为(x+4)元,根据题意,得
$\frac{1000}{x}-25=\frac{1000(1+20%)}{x+4}$.
整理,得x2+12x-160=0.
解得x1=8,x2=-20.
经检验:x1=8,x2=-20是原方程的解,x2=-20不合题意,舍去.
∴x=8.
答:七年级人均捐款数为8元.
点评 本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,解答时由八年级学生人数比七年级学生人数少25名建立方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.为了解某毕业班学生的睡眠时间情况,小红随机调查了该班15名同学,结果如表,则这15名同学每天睡眠时间的众数是8小时,中位数是8小时.
| 每天睡眠时间(单位:小时) | 7 | 7.5 | 8 | 8.5 | 9 |
| 人 数 | 2 | 4 | 5 | 3 | 1 |
12.计算:(-$\frac{1}{3}$x2y)3,结果正确的是( )
| A. | -$\frac{{x}^{6}{y}^{3}}{9}$ | B. | -$\frac{{x}^{5}y}{9}$ | C. | -$\frac{{x}^{6}{y}^{3}}{27}$ | D. | $\frac{{x}^{5}y}{27}$ |
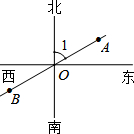 如图,已知A、B、O三点在同一条直线上,∠1=60°,则射线OA是表示北偏东60°方向的一条射线;射线OB是表示南偏西60°方向的一条射线.
如图,已知A、B、O三点在同一条直线上,∠1=60°,则射线OA是表示北偏东60°方向的一条射线;射线OB是表示南偏西60°方向的一条射线.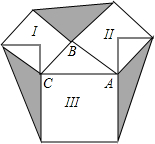 如图,若Rt△ABC的两直边AB=3,BC=2,Ⅰ,Ⅱ,Ⅲ分别表示以AB,BC,AC为边的正方形,则图中三个阴影部分面积之和为9.
如图,若Rt△ABC的两直边AB=3,BC=2,Ⅰ,Ⅱ,Ⅲ分别表示以AB,BC,AC为边的正方形,则图中三个阴影部分面积之和为9.