题目内容
已知∠AOB=α,∠BOC=β,(α>β),且OD,OE分别为∠AOB,∠BOC的角平分线,则∠DOE的度数为 (结果用α,β的代数式表示).
考点:角平分线的定义
专题:
分析:需要分类讨论:射线OC在∠AOB的内部和射线OC在∠AOB的外部两种情况.以第一种情况为例进行解答:
如图1:利用角平分线线的定义求得∠BOD=
∠AOB=
(α+β),同理知∠EOB=
∠BOC=
β,易求∠DOE=∠BOD-∠EOB.同理,如图2,易求∠DOE=∠BOD+∠EOB.
如图1:利用角平分线线的定义求得∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: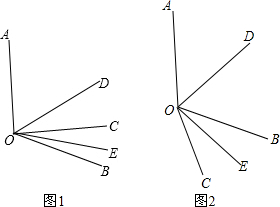 解:①如图1,∵∠AOC=α,∠BOC=β,且OD,OE分别为∠AOB,∠BOC的角平分线,
解:①如图1,∵∠AOC=α,∠BOC=β,且OD,OE分别为∠AOB,∠BOC的角平分线,
∴∠BOD=
∠AOB=
(α+β),∠EOB=
∠BOC=
β,
∴∠DOE=∠DOB-∠EOB=
(α+β)-
β=
α.
②如图2,∠DOE=∠DOB-∠EOB=
(α+β)+
β=
α+β.
综上所述,∠DOE的度数为
α或
α+β.
故答案是:
α或
α+β.
 解:①如图1,∵∠AOC=α,∠BOC=β,且OD,OE分别为∠AOB,∠BOC的角平分线,
解:①如图1,∵∠AOC=α,∠BOC=β,且OD,OE分别为∠AOB,∠BOC的角平分线,∴∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠DOB-∠EOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②如图2,∠DOE=∠DOB-∠EOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,∠DOE的度数为
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了角平分线线的定义.解题时,注意结合图形求得角与角间的和差关系:∠DOE=∠BOD-∠EOB或∠DOE=∠BOD+∠EOB.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
若方程(m2-1)x2-(m-1)x-8=0是关于x的一元一次方程,则m的值为( )
| A、-1 | B、1 | C、±1 | D、0 |
下列多项式中,不能用公式法因式分解的是( )
| A、x2+xy | ||
| B、x2+2xy+y2 | ||
| C、-x2+y2 | ||
D、
|
2014年1月1日零点,北京、南京、成都、银川的气温分别是-3℃,5℃,6℃,-7℃.当时这四个城市中,气温最低的是( )
| A、北京 | B、南京 | C、成都 | D、银川 |
 一个几何体的展开图如图所示,则这个几何体是( )
一个几何体的展开图如图所示,则这个几何体是( )| A、三棱锥 | B、四棱锥 |
| C、三棱柱 | D、四棱柱 |
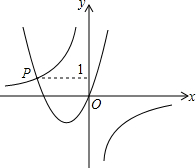 如图,函数y=
如图,函数y=