题目内容
13.已知:x+y+z≠0,a=$\frac{x}{y+z}$,b=$\frac{y}{x+z}$,c=$\frac{z}{x+y}$,求$\frac{a}{a+1}$+$\frac{b}{b+1}$+$\frac{c}{c+1}$的值.分析 先由a=$\frac{x}{y+z}$,b=$\frac{y}{x+z}$,c=$\frac{z}{x+y}$得xx=ay+az①,y=bx+bz②,z=cx+cy③,三式相加得出x+y+z=(b+c)x+(a+c)y+(a+b)z,从而得出$\left\{\begin{array}{l}{b+c=1}\\{a+c=1}\\{a+b=1}\end{array}\right.$,解得a=b=c=$\frac{1}{2}$,再把a、b、c的值都代入所求式子计算即可.
解答 解:∵a=$\frac{x}{y+z}$,b=$\frac{y}{x+z}$,c=$\frac{z}{x+y}$,
∴x=ay+az①,y=bx+bz②,z=cx+cy③,
①+②+③得,x+y+z=(b+c)x+(a+c)y+(a+b)z,
∴$\left\{\begin{array}{l}{b+c=1}\\{a+c=1}\\{a+b=1}\end{array}\right.$,解得a=b=c=$\frac{1}{2}$,
∴$\frac{a}{a+1}$+$\frac{b}{b+1}$+$\frac{c}{c+1}$=3×$\frac{\frac{1}{2}}{\frac{1}{2}+1}$=1.
点评 本题考查了分式的化简求值.解题的关键是得出x+y+z=(b+c)x+(a+c)y+(a+b)z,求得a=b=c=$\frac{1}{2}$.

练习册系列答案
相关题目
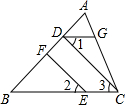 如图,CD⊥AB于D,E是BC上一点,EF⊥AB于F,∠1=∠2.试说明∠BDG+∠B=180°.
如图,CD⊥AB于D,E是BC上一点,EF⊥AB于F,∠1=∠2.试说明∠BDG+∠B=180°. 如图所示,回答下列问题:
如图所示,回答下列问题: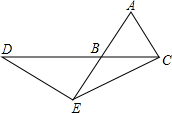 等边三角形ABC的边长为1,点D在直线BC上,点E在直线AB上,且AE=2.若△ECD是以CD为底的等腰三角形,则CD的长为3.
等边三角形ABC的边长为1,点D在直线BC上,点E在直线AB上,且AE=2.若△ECD是以CD为底的等腰三角形,则CD的长为3.