题目内容
以下列各组数为三角形三边长,能构成直角三角形的一组是( )
| A、8,15,17 |
| B、2,4,5 |
| C、6,8,12 |
| D、4,5,6 |
考点:勾股定理的逆定理
专题:
分析:根据勾股定理的逆定理对各选项进行逐一判断即可.
解答:解:A、∵82+152=289=172,∴能够成直角三角形,故本选项正确;
B、∵22+42=20≠52,∴不能够成直角三角形,故本选项错误;
C、∵62+82=100≠122,∴不能够成直角三角形,故本选项错误;
D、∵42+52=41≠62,∴不能够成直角三角形,故本选项错误.
故选A.
B、∵22+42=20≠52,∴不能够成直角三角形,故本选项错误;
C、∵62+82=100≠122,∴不能够成直角三角形,故本选项错误;
D、∵42+52=41≠62,∴不能够成直角三角形,故本选项错误.
故选A.
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
相关题目
 图中几何体的左视图是( )
图中几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
已知△ABC中,AB=17,AC=10,BC边上的高AD=8,则边BC的长为( )
| A、21 | B、15 | C、6 | D、21或9 |
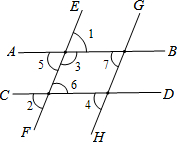 将依据填到相应的括号内:
将依据填到相应的括号内: 已知二次函数y=x2-2x-3
已知二次函数y=x2-2x-3