题目内容
已知△ABC中，AB=17，AC=10，BC边上的高AD=8，则边BC的长为（ ）
| A、21 | B、15 | C、6 | D、21或9 |
考点：勾股定理
专题：
分析：高线AD可能在三角形的内部也可能在三角形的外部，本题应分两种情况进行讨论．分别依据勾股定理即可求解．
解答：
解：如图所示，在Rt△ABD中，
∵AB=17，AD=8，
∴BD=
=15；
在Rt△ACD中，
∵AC=10，AD=8，
∴CD=
=6，
∴当AD在三角形的内部时，BC=15+6=21；
当AD在三角形的外部时，BC=15-6=9．
∴BC的长是21或9．
故选D．
解：如图所示，在Rt△ABD中，∵AB=17，AD=8，
∴BD=
| 172-82 |
在Rt△ACD中，
∵AC=10，AD=8，
∴CD=
| 102-82 |
∴当AD在三角形的内部时，BC=15+6=21；
当AD在三角形的外部时，BC=15-6=9．
∴BC的长是21或9．
故选D．
点评：本题考查的是勾股定理，在解答此题时要进行分类讨论，不要漏解．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
以下列各组数为三角形三边长，能构成直角三角形的一组是（ ）
| A、8，15，17 |
| B、2，4，5 |
| C、6，8，12 |
| D、4，5，6 |
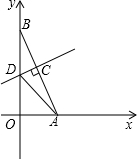已知如图，在平面直角坐标系中，点A、B分别在x轴、y轴上，线段OA、OB的长（OA＜OB）是方程x2-18x+72=0的两个根，且AC：BC=3：2，过点C作AB的垂线交y轴于点D．
如图所示，已知∠AOB=∠COD=90°，找出图中其他相等的角及图中互余的角．