题目内容
 将依据填到相应的括号内:
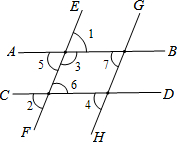
将依据填到相应的括号内:已知,如图,直线AB、CD、EF、GH,∠1=∠2,∠3+∠4=180°,求证:EF∥GH.
证明:因为∠1=∠2(已知)
又因为∠1=∠5
所以∠2=∠5
所以AB∥CD
所以∠3+∠6=180°
因为∠3+∠4=180°(已知)
所以∠4=∠6
所以EF∥GH
考点:平行线的判定与性质
专题:推理填空题
分析:根据平行线的判定与性质进行填空.
解答:证明:因为∠1=∠2(已知)
又因为∠1=∠5 (对顶角相等)
所以∠2=∠5 (等量代换)
所以AB∥CD (同位角相等,两直线平行)
所以∠3+∠6=180° (两直线平行,同旁内角互补)
因为∠3+∠4=180°(已知)
所以∠4=∠6 (等量代换)
所以EF∥GH (内错角相等,两直线平行).
故答案是:(对顶角相等);(等量代换);(同位角相等,两直线平行);(两直线平行,同旁内角互补);(等量代换);(内错角相等,两直线平行).
又因为∠1=∠5 (对顶角相等)
所以∠2=∠5 (等量代换)
所以AB∥CD (同位角相等,两直线平行)
所以∠3+∠6=180° (两直线平行,同旁内角互补)
因为∠3+∠4=180°(已知)
所以∠4=∠6 (等量代换)
所以EF∥GH (内错角相等,两直线平行).
故答案是:(对顶角相等);(等量代换);(同位角相等,两直线平行);(两直线平行,同旁内角互补);(等量代换);(内错角相等,两直线平行).
点评:本题考查了平行线的判定与性质.平行线的判定与性质的联系与区别
区别:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.
联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关.
区别:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.
联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关.

练习册系列答案
相关题目
以下列各组数为三角形三边长,能构成直角三角形的一组是( )
| A、8,15,17 |
| B、2,4,5 |
| C、6,8,12 |
| D、4,5,6 |
 如图,已知点B在x轴的负半轴上,AB⊥x轴于点B,AB=1,∠AOB=30°,求点A的坐标.
如图,已知点B在x轴的负半轴上,AB⊥x轴于点B,AB=1,∠AOB=30°,求点A的坐标.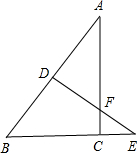 已知:如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交AB于点D,交AC于F,交BC的延长线于点E.
已知:如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交AB于点D,交AC于F,交BC的延长线于点E.
 如图,在?ABCD中,E,F分别为边AB和CD的中点,连接DE,BF,且AB=2AD=4
如图,在?ABCD中,E,F分别为边AB和CD的中点,连接DE,BF,且AB=2AD=4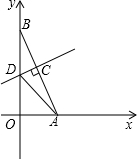 已知如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,且AC:BC=3:2,过点C作AB的垂线交y轴于点D.
已知如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,且AC:BC=3:2,过点C作AB的垂线交y轴于点D.