题目内容
 已知二次函数y=x2-2x-3
已知二次函数y=x2-2x-3(1)用配方法将y=x2-2x-3化成y=a(x-h)2的形式
(2)在图所给的平面直角坐标系中,画出这个二次函数的图象;
(3)根据图象回答:当自变量x的取值范围满足什么条件时,y>0?
考点:二次函数的三种形式,二次函数的图象
专题:
分析:(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
(2)利用描点法画出图象即可.
(3)利用y为正值则对应图象在x轴上方,进而得出x的取值范围.
(2)利用描点法画出图象即可.
(3)利用y为正值则对应图象在x轴上方,进而得出x的取值范围.
解答:解:(1)y=x2-2x-3
=x2-2x+1-4
=(x-1)2-4,
即y=(x-1)2-4;
(2)列表如下:
描点画图:

(3)如图所示,当x<-1或x>3时,y>0.
=x2-2x+1-4
=(x-1)2-4,
即y=(x-1)2-4;
(2)列表如下:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | -3 | 0 | … |

(3)如图所示,当x<-1或x>3时,y>0.
点评:本题主要考查了二次函数图象上点的坐标特征,二次函数的图象,抛物线与X轴的交点等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
以下列各组数为三角形三边长,能构成直角三角形的一组是( )
| A、8,15,17 |
| B、2,4,5 |
| C、6,8,12 |
| D、4,5,6 |

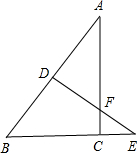 已知:如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交AB于点D,交AC于F,交BC的延长线于点E.
已知:如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交AB于点D,交AC于F,交BC的延长线于点E.
 如图,在?ABCD中,E,F分别为边AB和CD的中点,连接DE,BF,且AB=2AD=4
如图,在?ABCD中,E,F分别为边AB和CD的中点,连接DE,BF,且AB=2AD=4 阅读下列材料,并解答以下问题.
阅读下列材料,并解答以下问题.