题目内容
 如图,过矩形ABCD对角线AC的中点O作EF⊥AC,分别交AB、DC于E、F,点G为AE的中点,若∠AOG=30°,求证:OG=
如图,过矩形ABCD对角线AC的中点O作EF⊥AC,分别交AB、DC于E、F,点G为AE的中点,若∠AOG=30°,求证:OG=| 1 |
| 3 |
考点:矩形的性质,含30度角的直角三角形,直角三角形斜边上的中线
专题:证明题
分析:连接OB,利用在直角三角形中,斜边上的中线等于斜边的一半可得:AG=OG,再由已知条件可得△OEG是正三角形,进而证明△OEB是等腰三角形,得到OG=AG=GE=EB=OE,问题得证.
解答:证明:连接OB,
∵EF⊥AC,
∴△AOE是直角三角形
∴OG=AG=GE,
∴∠BAC=∠AOG=30°,∠AEO=60°,∠GOE=∠AOE-∠AOG=60°,
∴△OEG是正三角形,
∴OG=OE=GE,
∴∠ABO=∠BAC=30°,
∴∠AOB=180°-30°-30°=120°,
∴∠BOE=∠AOB-90°=30°,
∴△OEB是等腰三角形,
∴OE=EB,
∴OG=AG=GE=EB=OE,
∴OG=
AB=
DC.
∵EF⊥AC,

∴△AOE是直角三角形
∴OG=AG=GE,
∴∠BAC=∠AOG=30°,∠AEO=60°,∠GOE=∠AOE-∠AOG=60°,
∴△OEG是正三角形,
∴OG=OE=GE,
∴∠ABO=∠BAC=30°,
∴∠AOB=180°-30°-30°=120°,
∴∠BOE=∠AOB-90°=30°,
∴△OEB是等腰三角形,
∴OE=EB,
∴OG=AG=GE=EB=OE,
∴OG=
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查了矩形的性质和直角三角形的性质①在直角三角形中,30°角所对的直角边等于斜边的一半;②在直角三角形中,斜边上的中线等于斜边的一半.(即直角三角形的外心位于斜边的中点).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
有面额为壹元、贰元、伍元的人民币共10张,欲用来购买一盏价值为18元的护眼灯,要求三种面额都用上,则不同的付款方式有( )
| A、3种 | B、4种 | C、7种 | D、8种 |
某工厂今年计划产值为a万元,比去年增长11%.如果今年实际产值可超过计划1%,那么实际产值将比去年增长( )
| A、11% | B、11.1% |
| C、12% | D、12.11% |
 如图,已知△ABC中,D为BC中点,E,F为AB边三等分点,AD分别交CE,CF于点M,N,则AM:MN:ND等于
如图,已知△ABC中,D为BC中点,E,F为AB边三等分点,AD分别交CE,CF于点M,N,则AM:MN:ND等于 数形结合思想是中学数学解题中常用的数学思想,利用这种思想,可以将代数问题转化为几何问题,也可以将几何问题转化为代数问题.通过数形结合将代数与几何完美的结合在一起,可以大大降低解题的难度,提高效率和正确率,甚至还可以达到令人意想不到的效果.教科书中利用几何图形证明乘法公式(a+b)2=a2+2ab+b2的做法,就是一个非常典型的例子:
数形结合思想是中学数学解题中常用的数学思想,利用这种思想,可以将代数问题转化为几何问题,也可以将几何问题转化为代数问题.通过数形结合将代数与几何完美的结合在一起,可以大大降低解题的难度,提高效率和正确率,甚至还可以达到令人意想不到的效果.教科书中利用几何图形证明乘法公式(a+b)2=a2+2ab+b2的做法,就是一个非常典型的例子: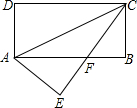 如图,ABCD为矩形,AB=a,BC=b(a>b),以对角线AC为对称轴将△ADC沿AC对折,则D点转移到E处,CE与AB交于F,则△AFC的面积为
如图,ABCD为矩形,AB=a,BC=b(a>b),以对角线AC为对称轴将△ADC沿AC对折,则D点转移到E处,CE与AB交于F,则△AFC的面积为 如图,直线y=x向下平移b个单位后得直线l,l与函数
如图,直线y=x向下平移b个单位后得直线l,l与函数