题目内容
在学校“阳光一小时”活动中,有A、B、C、D四名学生进行羽毛球双打比赛,并且以抽签的方式分成两组,其中A、B两名同学希望分到一组.
(1)请求A、B分到同一组的概率;
(2)若除A、B、C、D四名学生外,又有E、F两名同学要求参加,并且以抽签的方式分成3组,则A或B不与E或F分到同一组的概率是 ;
(3)若除A、B、C、D四名学生外,又有2n名同学要求参加(n为正整数),并且以抽签的方式分组,已知A、B分到同一组的概率是
,求n的值.
(1)请求A、B分到同一组的概率;
(2)若除A、B、C、D四名学生外,又有E、F两名同学要求参加,并且以抽签的方式分成3组,则A或B不与E或F分到同一组的概率是
(3)若除A、B、C、D四名学生外,又有2n名同学要求参加(n为正整数),并且以抽签的方式分组,已知A、B分到同一组的概率是
| 1 |
| 28 |
考点:列表法与树状图法
专题:
分析:(1)列举出符合题意的各种情况的个数和A,B都在同一组的结果种数,再根据概率公式解答即可.
(2)列举出符合题意的各种情况的个数和A或B不与E或F分到同一组的结果种数,再根据概率公式解答即可.
(3)根据已知得出A、B分到同一组的概率公式为
,进而求出即可.
(2)列举出符合题意的各种情况的个数和A或B不与E或F分到同一组的结果种数,再根据概率公式解答即可.
(3)根据已知得出A、B分到同一组的概率公式为
| 2 |
| (4+2n)(3+2n) |
解答:解:(1)
根据题意可得出:所有组合有:AB,AC,AD,BC,BD,CD,总共有6种结果,每种结果出现的可能性相同.
所有的结果中,满足A,B都在同一组的结果有1种,
所以A,B都在同一组的概率是
.
(2)根据题意可得出:
ABCDEF先把与A同组找到(共5类),再把其余4个人分2组(每类3种),共5×3=15种情况,
就是:①AB(CDEF重复上述ABCD分组,共3种情况:CD/EF;CE/DF;CF/DE)
②AC(BDEF:BD/EF;BE/DF;BF/DE)
③AD:3种(BCEF:BC/EF;BE/CF;BF/CE)
④AE:3种…
⑤AF:3种…
其中,①中3种+②中1种+③中1种=5种,
∴P(A或B不与E或F分到同一组)=
=
;
(3)根据题意得出:
=
,
解得:n1=2,n2=-
(舍去).
答:n的值为2.
根据题意可得出:所有组合有:AB,AC,AD,BC,BD,CD,总共有6种结果,每种结果出现的可能性相同.
所有的结果中,满足A,B都在同一组的结果有1种,
所以A,B都在同一组的概率是
| 1 |
| 6 |
(2)根据题意可得出:
ABCDEF先把与A同组找到(共5类),再把其余4个人分2组(每类3种),共5×3=15种情况,
就是:①AB(CDEF重复上述ABCD分组,共3种情况:CD/EF;CE/DF;CF/DE)
②AC(BDEF:BD/EF;BE/DF;BF/DE)
③AD:3种(BCEF:BC/EF;BE/CF;BF/CE)
④AE:3种…
⑤AF:3种…
其中,①中3种+②中1种+③中1种=5种,
∴P(A或B不与E或F分到同一组)=
| 5 |
| 15 |
| 1 |
| 3 |
(3)根据题意得出:
| 2 |
| (4+2n)(3+2n) |
| 1 |
| 28 |
解得:n1=2,n2=-
| 11 |
| 2 |
答:n的值为2.
点评:此题考查了概率公式与列表法或树状图法求概率.列表法或树状图法可以不重不漏的列举出所有可能发生的情况,列举法适合于两步完成的事件,树状图法适合于两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
在△ABC中,∠B=45°,∠C=60°,则
的值是( )
| AC |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,其中∠A+∠B+∠C+∠D+∠E+∠F+∠G=( )
如图所示,其中∠A+∠B+∠C+∠D+∠E+∠F+∠G=( )| A、180° | B、225° |
| C、360° | D、120° |

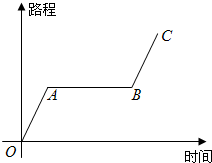 如图描述了秦宁放学回家的行程情况.根据上图回答问题:
如图描述了秦宁放学回家的行程情况.根据上图回答问题: 如图,过矩形ABCD对角线AC的中点O作EF⊥AC,分别交AB、DC于E、F,点G为AE的中点,若∠AOG=30°,求证:OG=
如图,过矩形ABCD对角线AC的中点O作EF⊥AC,分别交AB、DC于E、F,点G为AE的中点,若∠AOG=30°,求证:OG=