题目内容
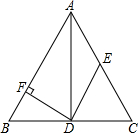 如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E为AC上一点,且AE=DE.
如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E为AC上一点,且AE=DE.(1)求证:DF⊥DE;
(2)若∠ABC+∠AED=180°,求证:AB+AE=2AF.
考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:(1)易证∠BAD=∠CAD和∠CAD=∠ADE,可得∠BAD=∠ADE,即可证明DE∥AB,即可解题;
(2)过D作DG⊥AC,可证∠ABC=∠DEG,AF=AG,即可证明△DFB≌△DGE,可得BF=EG,即可解题.
(2)过D作DG⊥AC,可证∠ABC=∠DEG,AF=AG,即可证明△DFB≌△DGE,可得BF=EG,即可解题.
解答:证明:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AE=DE,∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴DE∥AB,
∵DF⊥AB,
∴DF⊥DE;
(2)过D作DG⊥AC,

∵AD平分∠BAC,DF⊥AB,DG⊥AC,
∴DF=DG,∠DFB=∠DGE=90°,
∴AF=AG,
∵∠ABC+∠AED=180°,∠DEG+∠AED=180°,
∴∠ABC=∠DEG,
∵在△DFB和△DGE中,
,
∴△DFB≌△DGE,(AAS)
∴BF=EG,
∴AB+AE=AF+BF+AE=AF+EG+AE=AF+AG=2AF.
即AB+AE=2AF.
∴∠BAD=∠CAD,
∵AE=DE,∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴DE∥AB,
∵DF⊥AB,
∴DF⊥DE;
(2)过D作DG⊥AC,

∵AD平分∠BAC,DF⊥AB,DG⊥AC,
∴DF=DG,∠DFB=∠DGE=90°,
∴AF=AG,
∵∠ABC+∠AED=180°,∠DEG+∠AED=180°,
∴∠ABC=∠DEG,
∵在△DFB和△DGE中,
|
∴△DFB≌△DGE,(AAS)
∴BF=EG,
∴AB+AE=AF+BF+AE=AF+EG+AE=AF+AG=2AF.
即AB+AE=2AF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△DFB≌△DGE是解题的关键.

练习册系列答案
相关题目
给出下列各数:-3,0,+5,-3
,+3.1,-
,2004,+2010;其中是负数的有 ( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,若CM,BN是分别过点C,B的射线,且∠OCB=∠FCN,∠EBN=∠OBC,要使CM∥BN,则∠O需要满足什么条件?并说明理由.
如图,若CM,BN是分别过点C,B的射线,且∠OCB=∠FCN,∠EBN=∠OBC,要使CM∥BN,则∠O需要满足什么条件?并说明理由.