题目内容
已知点A(-2,-c)向右平移8个单位得A′,A与A′两点均在抛物线y=ax2+bx+c上,且这条抛物线与y轴的交点的纵坐标为-6,求抛物线的解析式.
考点:待定系数法求二次函数解析式
专题:
分析:根据平移可得到A′的坐标.与y轴的交点的纵坐标为-6,即抛物线中的c为-6,把A,A′坐标代入抛物线解析式即可.
解答:解:由抛物线y=ax2+bx+c与y轴交点的纵坐标为-6,得c=-6.
∴A(-2,6),点A向右平移8个单位得到点A′(6,6).
∵A与A′两点均在抛物线上,
∴
,解这个方程组,得
,
故抛物线的解析式是y=x2-4x-6.
∴A(-2,6),点A向右平移8个单位得到点A′(6,6).
∵A与A′两点均在抛物线上,
∴
|
|
故抛物线的解析式是y=x2-4x-6.
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组的解法,有一定难度.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
若
+|b+2|=0,则点M(a,b)的坐标是( )
| a-3 |
| A、(3,2) |
| B、(-3,2) |
| C、(3,-2) |
| D、(-3,-2) |
 如图利用一面长度为10米的墙.在用20米长的篱笆能围成一个面积为60平方米的矩形场地吗?若能,求出该场地与墙垂直的一边的长?若不能说明理由.
如图利用一面长度为10米的墙.在用20米长的篱笆能围成一个面积为60平方米的矩形场地吗?若能,求出该场地与墙垂直的一边的长?若不能说明理由.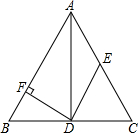 如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E为AC上一点,且AE=DE.
如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E为AC上一点,且AE=DE.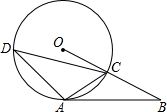 已知:如图,A是⊙O上的一点,半径OC的延长线与过点A的直径交于点B,OC=BC,AC=
已知:如图,A是⊙O上的一点,半径OC的延长线与过点A的直径交于点B,OC=BC,AC=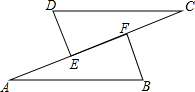 如图,DE⊥AC于E,BF⊥AC于F,AE=CF,CD=AB,求证:DC∥AB.
如图,DE⊥AC于E,BF⊥AC于F,AE=CF,CD=AB,求证:DC∥AB.