题目内容
一正方形的边长为10，将它缩小为原来的
，得到的新正方形面积为 ．
| 3 |
| 5 |
考点：相似多边形的性质
专题：计算题
分析：设新正方形的边长为x，根据相似多边形的性质得到
=
，求出x，然后利用正方形的面积公式求解．
| x |
| 10 |
| 3 |
| 5 |
解答：解：设新正方形的边长为x，
根据题意得
=
，
解得x=6，
所以新正方形面积=62=36．
故答案为36．
根据题意得
| x |
| 10 |
| 3 |
| 5 |
解得x=6，
所以新正方形面积=62=36．
故答案为36．
点评：本题考查了相似多边形的性质：对应角相等；对应边的比相等．
练习册系列答案
相关题目
若
+|b+2|=0，则点M（a，b）的坐标是（ ）
| a-3 |
| A、（3，2） |
| B、（-3，2） |
| C、（3，-2） |
| D、（-3，-2） |
如果a+b=0，那么a，b两个实数一定是（ ）
| A、都等于0 | B、一正一负 |
| C、互为相反数 | D、不确定 |
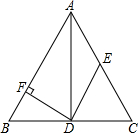如图，在△ABC中，AD平分∠BAC，DF⊥AB于点F，E为AC上一点，且AE=DE．
如图，AD⊥BD，BC⊥AC，AD=BC．求证：∠OAB=∠OBA．