题目内容
 如图,若CM,BN是分别过点C,B的射线,且∠OCB=∠FCN,∠EBN=∠OBC,要使CM∥BN,则∠O需要满足什么条件?并说明理由.
如图,若CM,BN是分别过点C,B的射线,且∠OCB=∠FCN,∠EBN=∠OBC,要使CM∥BN,则∠O需要满足什么条件?并说明理由.考点:平行线的判定
专题:
分析:当∠O=90°时,CM∥BN,根据三角形内角和可得∠OCB+∠OBC=90°,进而可得∠FCM+∠EBN=90°,然后根据平角定义可算出∠MCB+∠CBN=360°-90°-90°=180°,根据同旁内角互补,两直线平行可得CM∥BN.
解答:解:当∠O=90°时,CM∥BN,
∵∠O+∠OCB+∠OBC=180°,
∴∠OCB+∠OBC=90°,
∵∠OCB=∠FCN,∠EBN=∠OBC,
∴∠FCM+∠EBN=90°,
∵∠FCM+∠MCB+∠OCB+∠OBC+∠CBN+∠NBE=360°,
∴∠MCB+∠CBN=360°-90°-90°=180°,
∴CM∥BN.
∵∠O+∠OCB+∠OBC=180°,
∴∠OCB+∠OBC=90°,
∵∠OCB=∠FCN,∠EBN=∠OBC,
∴∠FCM+∠EBN=90°,
∵∠FCM+∠MCB+∠OCB+∠OBC+∠CBN+∠NBE=360°,
∴∠MCB+∠CBN=360°-90°-90°=180°,
∴CM∥BN.
点评:此题主要考查了平行线的判定,关键是正确推理出∠MCB+∠CBN=360°-90°-90°=180°.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
在
,
,
,
四个数中,无理数共有( )
| 4 |
| 3 | -9 |
| π |
| 3 |
| 355 |
| 113 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知x=1+2m,y=1+
,则y=( )
| 1 |
| 2m |
| A、x | ||
B、
| ||
C、
| ||
D、
|
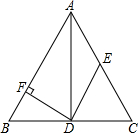 如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E为AC上一点,且AE=DE.
如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E为AC上一点,且AE=DE.