Question

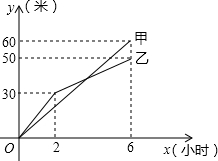甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度y（米）与挖掘时间x（小时）之间的关系如图，请根据图象所提供的信息解答下列问题：
（1）求：
①甲队在0≤x≤6的时段内，y与x之间的函数关系式；
②乙队在2≤x≤6的时段内，y与x之间的函数关系式；
（2）当x为何值时，甲、乙两队在施工过程中所挖河渠的长度相等？

Answer 1

考点：一次函数的应用

专题：

分析：（1）①设函数解析式为y=kx（k≠0），根据图象经过点（6，60），然后利用待定系数法求一次函数解析式解答；
②设函数解析式为y=ax+b（a≠0），根据函数图象经过点（2，30）和点（6，50），利用待定系数法求一次函数解析式解答；
（2）根据所挖河渠的长度相等，y值相等列出方程，然后求解即可．

解答：解：（1）①甲队在0≤x≤6的时段内，
根据题意，函数y=kx（k≠0）的图象经过点（6，60），
∴60=6k，
解得，k=10，
∴y=10x；
②乙队在2≤x≤6的时段内，
根据题意，函数y=ax+b（a≠0）的图象经过点（2，30）和点（6，50），
∴

2a+b=30 6a+b=50

，
解得

a=5 b=20

，
∴y=5x+20；

（2）根据题意得，10x=5x+20，
解方程得，x=4，
答：当x为4时，甲、乙两队在施工过程中所挖河渠的长度相等．

点评：本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，待定系数法求函数解析式是常用的方法，需熟练掌握并灵活运用．