题目内容
甲、乙两位棋手棋艺相当,他们在一项奖金为10000元的比赛中相遇,比赛为七局四胜制(无平局).已经进行了五局的比赛,结果为甲三胜二负.现在因故要停止比赛,问应该如何分配这10000元比赛奖金才算合理?
考点:列表法与树状图法
专题:
分析:首先设第6局、第7局的顺序为(x,y),则取胜有(甲,甲),(甲,乙),(乙,乙),(乙,甲)4种情况,则可求得甲、乙胜的概率,继而求得答案.
解答:解:设第6局、第7局的顺序为(x,y),
则取胜有(甲,甲),(甲,乙),(乙,乙),(乙,甲)4种情况,
∵其中甲胜有3种,乙胜有1种,
∴甲胜的概率为
,乙胜的概率为
,
∴甲得7500元、乙得2500元比赛奖金才算合理.
则取胜有(甲,甲),(甲,乙),(乙,乙),(乙,甲)4种情况,
∵其中甲胜有3种,乙胜有1种,
∴甲胜的概率为
| 3 |
| 4 |
| 1 |
| 4 |
∴甲得7500元、乙得2500元比赛奖金才算合理.
点评:此题考查了列举法求概率的知识.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若7名学生的体重(单位:kg)分别是:40,42,43,45,47,47,58,则这组数据的平均数是( )
| A、44 | B、45 | C、46 | D、47 |
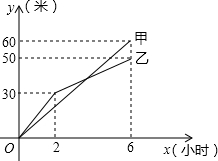 甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系如图,请根据图象所提供的信息解答下列问题:
甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系如图,请根据图象所提供的信息解答下列问题: 如图,在△ABC中,BG为高,点E、F、D分别在BC、AC、AB上,且EF⊥AC,∠1=∠2,∠ABC=60°,求∠ADG的度数.
如图,在△ABC中,BG为高,点E、F、D分别在BC、AC、AB上,且EF⊥AC,∠1=∠2,∠ABC=60°,求∠ADG的度数.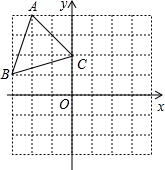 如图,三角形ABC中,A(-2,4),B(-3,1)、C(0,2),将三角形ABC先向右平移3个单位长度,再向下平移2个单位长度,得到三角形A′B′C′.
如图,三角形ABC中,A(-2,4),B(-3,1)、C(0,2),将三角形ABC先向右平移3个单位长度,再向下平移2个单位长度,得到三角形A′B′C′.