题目内容
6.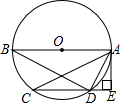 如图,在⊙O中,AB为直径,延长CD至E,使得AE⊥CE.
如图,在⊙O中,AB为直径,延长CD至E,使得AE⊥CE.(1)求证:△ABD∽△ACE;
(2)若AE与⊙O相切于点A,AE=4,CE=8,求直径AB的长度.
分析 (1)由AB为⊙O的直径,AE⊥CE,得到∠ADB=∠E=90°,根据圆周角定理得到∠B=∠C,于是得到△ABD∽△ACE;
(2根据已知条件证得△ACE∽△DAE,△ABD∽△ADE,列出比例式代入数值即可得到结论.
解答 (1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∵AE⊥CE,
∴∠E=90°,
∴∠ADB=∠E,
∵∠B=∠C,
∴△ABD∽△ACE;
(2)解:∵AE与⊙O相切于点A,
∴∠C=∠B=∠DAE,
∵∠E=∠E,
∴△ACE∽△DAE,
∴$\frac{AE}{DE}=\frac{CE}{AE}$,
∴DE=$\frac{{AE}^{2}}{CE}$=$\frac{{4}^{2}}{8}$=2,
∴AD=$\sqrt{{AE}^{2}{+DE}^{2}}$=2$\sqrt{5}$,
∵∠ADB=∠E,∠B=∠DAE,
∴△ABD∽△ADE,
∴$\frac{AD}{DE}=\frac{AB}{AD}$,
∴AB=$\frac{{AD}^{2}}{DE}$=10.
点评 本题考查了切线的性质,相似三角形的判定和性质,勾股定理,圆周角定理,弦切角定理,找准相似三角形是解题的关键.

练习册系列答案
相关题目
14.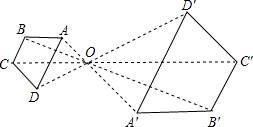 如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为( )
如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为( )
 如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为( )
如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为( )| A. | 1:2 | B. | 1:4 | C. | 2:1 | D. | 4:1 |
11.下面几个几何体,主视图是圆的是( )
| A. |  | B. |  | C. |  | D. |  |
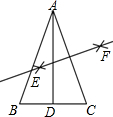 如图,△ABC中,AB=AC,AD是BC边中线,分别以点A、C为圆心,以大于$\frac{1}{2}$AC长为半径画弧,两弧交点分别为点E、F,直线EF与AD相交于点O,若OA=2,则△ABC外接圆的面积为4π.
如图,△ABC中,AB=AC,AD是BC边中线,分别以点A、C为圆心,以大于$\frac{1}{2}$AC长为半径画弧,两弧交点分别为点E、F,直线EF与AD相交于点O,若OA=2,则△ABC外接圆的面积为4π.
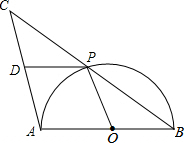 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.