题目内容
1.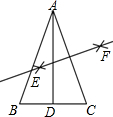 如图,△ABC中,AB=AC,AD是BC边中线,分别以点A、C为圆心,以大于$\frac{1}{2}$AC长为半径画弧,两弧交点分别为点E、F,直线EF与AD相交于点O,若OA=2,则△ABC外接圆的面积为4π.
如图,△ABC中,AB=AC,AD是BC边中线,分别以点A、C为圆心,以大于$\frac{1}{2}$AC长为半径画弧,两弧交点分别为点E、F,直线EF与AD相交于点O,若OA=2,则△ABC外接圆的面积为4π.
分析 利用等腰三角形的性质结合三角形外接圆的作法得出O点即为△ABC外接圆的圆心,进而求出其面积.
解答  解:∵AB=AC,AD是BC边中线,
解:∵AB=AC,AD是BC边中线,
∴AD垂直平分BC,
∵分别以点A、C为圆心,以大于$\frac{1}{2}$AC长为半径画弧,两弧交点分别为点E、F,
∴EF垂直平分AC,
∵直线EF与AD相交于点O,
∴点O即为△ABC外接圆圆心,
∴AO为△ABC外接圆半径,
∴△ABC外接圆的面积为:4π.
故答案为:4π.
点评 此题主要考查了三角形的外心,得出O点即为△ABC外接圆圆心是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
12.计算(-π)0,结果是( )
| A. | 0 | B. | -π | C. | -3.14 | D. | 1 |
9.下列图形中,中心对称图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.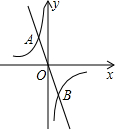 如图,函数y1=$\frac{{k}_{1}}{x}$(k1≠0)与y2=k2x(k2≠0)的图象Ox交于A、B两点,且A(-1,3).若y1<y2,则x的取值范围是( )
如图,函数y1=$\frac{{k}_{1}}{x}$(k1≠0)与y2=k2x(k2≠0)的图象Ox交于A、B两点,且A(-1,3).若y1<y2,则x的取值范围是( )
 如图,函数y1=$\frac{{k}_{1}}{x}$(k1≠0)与y2=k2x(k2≠0)的图象Ox交于A、B两点,且A(-1,3).若y1<y2,则x的取值范围是( )
如图,函数y1=$\frac{{k}_{1}}{x}$(k1≠0)与y2=k2x(k2≠0)的图象Ox交于A、B两点,且A(-1,3).若y1<y2,则x的取值范围是( )| A. | -1<x<0 | B. | x<-1或0<x<1 | C. | -1<x<1 | D. | -1<x<0或x>1 |
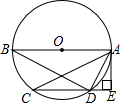 如图,在⊙O中,AB为直径,延长CD至E,使得AE⊥CE.
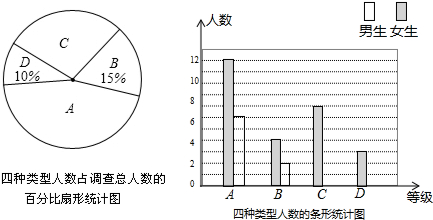
如图,在⊙O中,AB为直径,延长CD至E,使得AE⊥CE. 在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( ) 如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( )
如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( )


