题目内容
4. 如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B.
如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B.(1)求点A,点B的坐标;
(2)过点B平行x轴的直线交抛物线于点C,求四边形OACB的面积;
(3)是否存在点P,使以P,A,B,C为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
分析 (1)已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B.直接令x=0,和y=0求解即可;
(2)由过点B平行x轴的直线交抛物线于点C,确定出点C的坐标,求出BC,OA,OB,即可求出梯形的面积;
(3)分两种情况计算:①BC为边时,有BC=AP=4,且点P必在x轴上,设P(m,0),建立方程求解,②BC为对角线时,对角线PA和BC互相平分,设P(x,y)由中点坐标公式建立方程求解.
解答 解:(1)∵二次函数y=(x+2)2的图象与x轴交于点A,
∴令x=0,
∴y=4,
∴B(0,4)
∵二次函数y=(x+2)2的图象与y轴交于点B,
令y=0,
∴(x+2)2=0,
∴x=-2,
∴A(-2,0)
(2)∵过点B平行x轴的直线交抛物线于点C,
∴4=(x+2)2
∴x1=0,x2=-4,
∴C(-4,4),
∴BC=4,OB=4,OA=2,
∴S四边形OACB=$\frac{1}{2}$(OA+BC)×OB
=$\frac{1}{2}$×6×4
=12;
(3)①BC为边时,有BC=AP=4,且点P必在x轴上,设P(m,0),
∴AP=|m+2|,
∴|m+2|=4,
∴m1=2,m2=-6,
∴P1(2,0),P2(-6,0),
②BC为对角线时,对角线PA和BC互相平分,设P(x,y)
根据中点坐标公式得,-2+x=-2×2,0+y=4×2,
∴x=-2,y=8,
∴P3(-2,8).
即:满足条件的P点有三个,P1(2,0),P2(-6,0),P3(-2,8).
点评 此题是二次函数综合题,主要考查了特殊点的坐标的确定,梯形的面积公式,平行四边形的性质,解本题的关键是分情况解决问题的思想.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
1.某班数学兴趣小组收集了本市4月份30天的日最高气温的数据,经过统计分析获得了两条信息和一个统计表(天数为正整数).
信息1:4月份日最高气温的中位数是15.5℃;
信息2:4月份日最高气温的众数是17℃.
4月份日最高气温统计表
请根据上述信息求x,y,z的值.
信息1:4月份日最高气温的中位数是15.5℃;
信息2:4月份日最高气温的众数是17℃.
4月份日最高气温统计表
| 气温℃ | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 天数/天 | 2 | 3 | x | 5 | 4 | y | z | 3 | 2 | 3 |
2.甲、乙两名同学在参加体育中考前各作了5次投掷实心球的测试,甲、乙所测得的成绩的平均数相同,且甲、乙成绩的方差分别为0.62、0.72,那么( )
| A. | 甲、乙成绩一样稳定 | B. | 甲成绩更稳定 | ||
| C. | 乙成绩更稳定 | D. | 不能确定谁的成绩更稳定 |
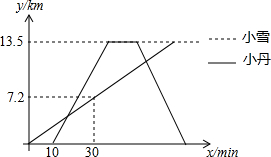 小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.
小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.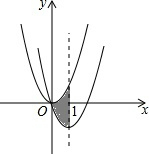 如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-1)2-1,其对称轴与两抛物线所围成的阴影部分的面积为1.
如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-1)2-1,其对称轴与两抛物线所围成的阴影部分的面积为1.