题目内容
2.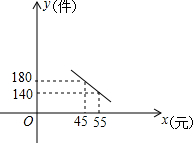 大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.(1)求y与x的函数关系式.
(2)设王强每月获得的利润为p(元),求p与x之间的函数关系式;如果王强想要每月获得最大的利润,那么销售单价应定为多少元?最大利润是多少元?
分析 (1)设y与x的函数关系式为:y=kx+b(k≠0),将(45,180),(55,140)代入,利用待定系数法即可求出一次函数解析式;
(2)根据题意列出二次函数关系式,再根据求二次函数最值的方法便可解出答案.
解答 解:(1)设y与x的函数关系式为:y=kx+b(k≠0),
由题意得,
$\left\{\begin{array}{l}{45k+b=180}\\{55k+b=140}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-4}\\{b=360}\end{array}\right.$.
故y与x的函数表达式为y=-4x+360(40≤x≤60).
(2)由题意得,p与x的函数关系式为:
p=(x-40)(-4x+360)=-4x2+520x-14400=-4(x-65)2+2500,
当x=65元时,最大利润是2500元.
点评 此题考查待定系数法求函数解析式、二次函数的性质及其应用,还考查抛物线的基本性质,另外将实际问题转化为求函数最值问题,从而来解决实际问题

练习册系列答案
相关题目
12.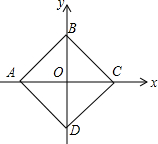 以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )
以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )
 以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )
以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )| A. | ($\sqrt{2}$,$\sqrt{2}$) | B. | ($\sqrt{2}$,-$\sqrt{2}$) | C. | (-1,1) | D. | (1,-1) |
10.下列函数中,y是x的正比例函数的是( )
| A. | y=2x-1 | B. | y=$\frac{3}{x}$ | C. | y=2x | D. | y=$\frac{2}{x}$ |
12.下列图形中,不是轴对称图形的是( )
| A. |  锐角 | B. |  等腰三角形 | C. |  直角三角形 | D. |  扇形 |
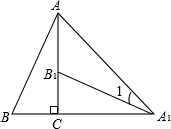 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是60°.
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是60°.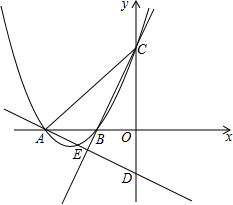 如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,
如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,