题目内容
15.如果实数x,y满足$\sqrt{x+1}$+|y-2|=0,则xy的值是-2.分析 根据实数x,y满足$\sqrt{x+1}$+|y-2|=0,可以求得x、y的值,从而可以求得xy的值,本题得以解决.
解答 解:∵实数x,y满足$\sqrt{x+1}$+|y-2|=0,
∴$\left\{\begin{array}{l}{x+1=0}\\{y-2=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,
∴xy=-2,
故答案为:-2.
点评 本题考查非负数的性质,解答本题的关键是求出x、y的值.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{6}$=3 | B. | $\sqrt{2}$×$\sqrt{6}$=3$\sqrt{2}$ | C. | $\sqrt{8}$÷$\sqrt{2}$=4 | D. | ($\sqrt{12}$-$\sqrt{3}$)×$\sqrt{3}$=3 |
 某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m,8m,现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩建后的等腰三角形花圃的周长.
某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m,8m,现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩建后的等腰三角形花圃的周长. 如图,AB∥CD,CB平分∠ABD,若∠C=35°,则∠D的度数为110°.
如图,AB∥CD,CB平分∠ABD,若∠C=35°,则∠D的度数为110°.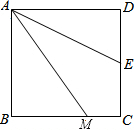 如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.
如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM. 如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有6个.
如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有6个.