题目内容
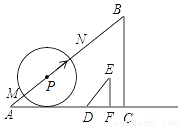
如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60cm,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿
CA方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与直线AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中:
(1)连接ME,当ME∥AC时,t=________s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目


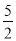 B. x>
B. x>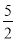 C. x<
C. x<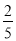 D. x<?
D. x<?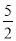
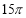 ,底面半径为3,则该圆锥的母线长为 .
,底面半径为3,则该圆锥的母线长为 .