题目内容
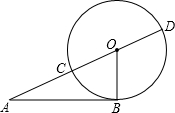 如图,在Rt△ABO中,∠B=Rt∠,以O为圆心,OB为半径画圆,分别交AO和AO的延长线于C、D,若OB=1,AB=3;
如图,在Rt△ABO中,∠B=Rt∠,以O为圆心,OB为半径画圆,分别交AO和AO的延长线于C、D,若OB=1,AB=3;(1)分别求AC、AD的长;
(2)判断AC•AD与AB的关系.
考点:二次根式的应用
专题:
分析:(1)利用勾股定理求得AO的长度;然后由AC=AO-OC=AO-OB求得AC的长度,由AD=AO+OB来求AD的长度;
(2)把AD、AC的长度代入求AC•AD,然后与AB2来比较.
(2)把AD、AC的长度代入求AC•AD,然后与AB2来比较.
解答:解:(1)根据勾股定理有:OA2=AB2+OB2,
∴OA=
=
,
∵OC=OB=OD=1,
∴AC=AO-OC=AO-OB,AD=AO+OB,
∴AC=
-1,AD=
+1;
(2)由(1)知,AC=
-1,AD=
+1,则AC•AD=(
-1)(
+1)=9
∵AB2=9,
∴AC•AD=AB2.
∴OA=
| AB2+OB2 |
| 10 |
∵OC=OB=OD=1,
∴AC=AO-OC=AO-OB,AD=AO+OB,
∴AC=
| 10 |
| 10 |
(2)由(1)知,AC=
| 10 |
| 10 |
| 10 |
| 10 |
∵AB2=9,
∴AC•AD=AB2.
点评:本题考查了二次根式的应用.涉及图形的问题要充分利用图形所提供的信息,如本题中结合题意来观察图形易知AB是圆O的切线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a、b为有理数,则多项式a2+b2-2a-6b+12的值为( )
| A、正数 | B、零 | C、负数 | D、非负数 |
 已知△ABC,
已知△ABC, 如图为6个边长相等的正方形的组合图形,则∠1+∠3=
如图为6个边长相等的正方形的组合图形,则∠1+∠3=