题目内容
5.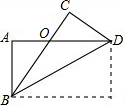 如图,矩形纸片ABCD的长为6$\sqrt{3}$cm,宽为6cm,将其沿对角线折叠,则其重叠部分的面积等于12$\sqrt{3}$cm2.
如图,矩形纸片ABCD的长为6$\sqrt{3}$cm,宽为6cm,将其沿对角线折叠,则其重叠部分的面积等于12$\sqrt{3}$cm2.
分析 先根据矩形的性质得AB=CD=6,AD=BC=6$\sqrt{3}$,AD∥BC,再根据折叠的性质得∠DBC=∠DBO,由AD∥BC得∠DBC=∠BDO,所以∠BDO=∠OBD,根据等腰三角形的判定得OB=OD,设OD=x,则OB=x,AO=4-x,在Rt△ABO中,根据勾股定理得到62+(6$\sqrt{3}$-x)2=x2,解得x=4$\sqrt{3}$,然后根据三角形面积公式求解.
解答  解:∵四边形ABCD为矩形,
解:∵四边形ABCD为矩形,
∴AB=CD=6,AD=BC=6$\sqrt{3}$,AD∥BC,
∵矩形纸片ABCD沿对角线BD折叠,
∴∠DBC=∠DBO,
∵AD∥BC,
∴∠DBC=∠BDO,
∴∠BDO=∠OBD,
∴OB=OD,
设OD=x,则OB=x,AO=4-x,
在Rt△ABO中,∵AB2+AO2=BO2,
∴62+(6$\sqrt{3}$-x)2=x2,
解得x=4$\sqrt{3}$,
∴DO=4$\sqrt{3}$,
∴△BOD的面积=$\frac{1}{2}$AB•DO=$\frac{1}{2}$×6×4$\sqrt{3}$=12$\sqrt{3}$cm2,
故答案为:12$\sqrt{3}$cm2.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
15.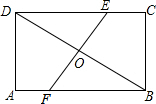 如图,在矩形ABCD中,AB=8,BC=6,EF是BD的中垂线,则EF=( )
如图,在矩形ABCD中,AB=8,BC=6,EF是BD的中垂线,则EF=( )
 如图,在矩形ABCD中,AB=8,BC=6,EF是BD的中垂线,则EF=( )
如图,在矩形ABCD中,AB=8,BC=6,EF是BD的中垂线,则EF=( )| A. | $\frac{15}{4}$ | B. | 5 | C. | 8 | D. | $\frac{15}{2}$ |
17.三元一次方程组$\left\{\begin{array}{l}{3x-2y=5}\\{x+y+z=2}\\{z=2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=1}\\{z=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\\{z=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\\{z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\\{z=2}\end{array}\right.$ |
14.△ABC的三边长分别为$\sqrt{2}$,$\sqrt{10}$和2,△A′B′C′的两边长分别为1和$\sqrt{5}$.如果△ABC∽△A′B′C′,则
△A′B′C′第三边的长为( )
△A′B′C′第三边的长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
15.2013年04月20日08时02分在四川省雅安市芦山县发生7.0级地震,震源深度13千米.能够准确表示芦山县这个地点位置的是( )
| A. | 北纬30.3° | B. | 东经103.0° | ||
| C. | 四川省雅安市 | D. | 北纬31°,东经103° |
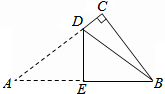 如图,已知Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.现将△ABC沿折痕DE进行折叠,使顶点A,B重合,则△DCB的周长等于14cm.
如图,已知Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.现将△ABC沿折痕DE进行折叠,使顶点A,B重合,则△DCB的周长等于14cm. 如图,△ABC三定点在圆O上,AC是圆O的直径,∠C=52°,∠ABC平分线BD交圆O于点D,求∠BAD的度数.
如图,△ABC三定点在圆O上,AC是圆O的直径,∠C=52°,∠ABC平分线BD交圆O于点D,求∠BAD的度数. 如图,直线AB⊥l1,l1∥l2,∠1=75°,则∠2的大小为165°.
如图,直线AB⊥l1,l1∥l2,∠1=75°,则∠2的大小为165°.