题目内容
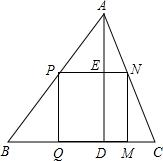 如图,△ABC是一块锐角三角形余料,其中BC=15cm,高AD=10cm,现在要把它裁剪成一个矩形材料备用,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,若矩形的一边PN=9,求矩形另一边PQ的长.
如图,△ABC是一块锐角三角形余料,其中BC=15cm,高AD=10cm,现在要把它裁剪成一个矩形材料备用,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,若矩形的一边PN=9,求矩形另一边PQ的长.考点:相似三角形的应用
专题:
分析:设PQ的长为xcm,根据矩形的性质可得ED=PQ=x,然后求出△APN和△ABC相似,再利用相似三角形对应高的比等于对应边的比列式计算即可得解.
解答:解:设PQ的长为xcm,
∵四边形PQMN是矩形,AD是高,
∴ED=PQ=x,
∵PN∥BC,
∴△APN∽△ABC,
∴
=
,
即
=
,
解得x=4.
所以,矩形另一边PQ的长为4cm.
∵四边形PQMN是矩形,AD是高,
∴ED=PQ=x,
∵PN∥BC,
∴△APN∽△ABC,
∴
| AE |
| AD |
| PN |
| BC |
即
| 10-x |
| 10 |
| 9 |
| 15 |
解得x=4.
所以,矩形另一边PQ的长为4cm.
点评:本题考查了相似三角形的应用,主要利用了相似三角形对应高的比等于对应边的比,熟记性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
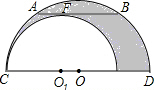 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,则阴影部分的面积是( )
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,则阴影部分的面积是( )| A、πcm2 |
| B、2πcm2 |
| C、3πcm2 |
| D、4πcm2 |
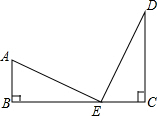 如图,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:
如图,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论: 如图,AB是半圆的直径,直线MN切半圆于C,同AM⊥MN,BN⊥MN,如果AM=6,BN=8,那么半圆的直径是
如图,AB是半圆的直径,直线MN切半圆于C,同AM⊥MN,BN⊥MN,如果AM=6,BN=8,那么半圆的直径是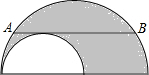 如图,大圆的弦AB与小圆相切,且小圆圆心在大圆直径上,若AB=12,则图中阴影部分的面积为
如图,大圆的弦AB与小圆相切,且小圆圆心在大圆直径上,若AB=12,则图中阴影部分的面积为