题目内容
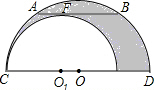 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,则阴影部分的面积是( )
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,则阴影部分的面积是( )| A、πcm2 |
| B、2πcm2 |
| C、3πcm2 |
| D、4πcm2 |
考点:切线的性质,勾股定理,垂径定理
专题:计算题
分析:作OE⊥AB于E,连接O1F,OB,如图,根据切线的性质得O1F⊥AB,再判断四边形OO1FE为矩形,得到OE=O1F,然后根据垂径定理得到BE=
AB=2,在Rt△OBE中,利用勾股定理得OB2-OE2=BE2=4,再利用阴影部分的面积=
S⊙0-
S⊙O1计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: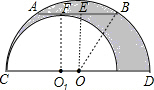 解:作OE⊥AB于E,连接O1F,OB,如图,
解:作OE⊥AB于E,连接O1F,OB,如图,
∵大半圆的弦AB与小半圆相切于F,
∴O1F⊥AB,
而OE⊥AB,AB∥CD,
∴四边形OO1FE为矩形,
∴OE=O1F,
∵OE⊥AB,
∴AE=BE=
AB=2,
在Rt△OBE中,OB2-OE2=BE2=4,
∵阴影部分的面积=
S⊙0-
S⊙O1=
(π•OB2-π•O1F2)=
π(OB2-OE2)=2π(cm2).
故选B.
 解:作OE⊥AB于E,连接O1F,OB,如图,
解:作OE⊥AB于E,连接O1F,OB,如图,∵大半圆的弦AB与小半圆相切于F,
∴O1F⊥AB,
而OE⊥AB,AB∥CD,
∴四边形OO1FE为矩形,
∴OE=O1F,
∵OE⊥AB,
∴AE=BE=
| 1 |
| 2 |
在Rt△OBE中,OB2-OE2=BE2=4,
∵阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了两圆相切的性质、勾股定理和垂径定理.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
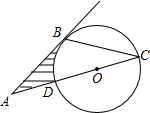 如图,AB为⊙O的切线,切点为点B,切线BA与直径CD的延长线相交于点A,CD=4,∠A=30°,则图中阴影部分的面积为
如图,AB为⊙O的切线,切点为点B,切线BA与直径CD的延长线相交于点A,CD=4,∠A=30°,则图中阴影部分的面积为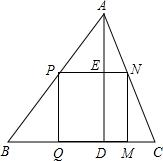 如图,△ABC是一块锐角三角形余料,其中BC=15cm,高AD=10cm,现在要把它裁剪成一个矩形材料备用,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,若矩形的一边PN=9,求矩形另一边PQ的长.
如图,△ABC是一块锐角三角形余料,其中BC=15cm,高AD=10cm,现在要把它裁剪成一个矩形材料备用,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,若矩形的一边PN=9,求矩形另一边PQ的长.